Счётная компактность топологического пространства

[maxmatem]

Всякое компактное топологическое пространство, счётно компактно.
Допустим, что это не так.

Рассмотрим топологическое пространство $X$, и в $Y\subset X$ выделем счётное подмножество $M$ , $M\subset Y$,
$\[M = \{ {x_1},{x_2},...,{x_n}...\} \]$
в котором нет предельных точек. тогда построим следующее семейство замкнутых подмножеств $\[\Im = \{ {F_n}\} ,n \in \mathbb{N},{F_n} = [{M_n}]\]$
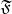
и очевидно что семейство $\mathfrak{F}$ имеет пустое пересечение.Допустим ,что это не так $ \[\bigcap\limits_{i = 1}^\infty {{F_i}} \ne \emptyset \]$, значит $\[p \in \bigcap\limits_{i = 1}^\infty {{F_i}} \]$, тогда $\[\forall {F_n}\forall n \in \mathbb{N} \Rightarrow {U_n}(p)\bigcap {{M_n} \ne \emptyset } \]$, т.е окресность точки $p$ содержит бесконечно много точек из $M$ значит точка $p$-предельная для множества $M$, но это противоречит нашему предположению что в $M$ нет предельных точек. Тогда семейство $\[\{ \Im \} \]$ является центрированым семейством, и оно имеет пустое пересечение $\[\bigcap\limits_{i = 1}^\infty {{F_i}} = \emptyset \]$, тогда пространство $X$-некомпактное, но это противоречит условию теоремы!

Вопрос у меня возник, из каких соображений $\[\{ \Im \} \]$, будет центрированым? разве $\[\bigcap\limits_{i = 1}^n {{F_i}} \ne \emptyset \]$ ?

[Padawan]

А определением компактности через открытые покрытия не проще воспользоваться? Получается вообще тавтология. Из любого покрытия можно выделить конечное подпокрытие (компактность) -> из счетного покрытия можно выделить конечное подпокрытие (счетная компактность)

[maxmatem]

Да! но меня интересовало именно эта теорема и её доказательство, почему оно центрированое семейство? до этого я доказывал эквивалентность того что, топологическое пространство счётно компактно эквивалентно тому что всякое счётная центрированое семейство замкнутых подмножеств имеет не пустое пересечение.(кстати в доказательстве данной теоремы проблем не возникло ). так почему это семейство центрированое ?
кстати то рассуждение которое вы провели надо доказать!(я пока до этой леммы ещё не дошел...), но я думаю, что докажу!

[Padawan]

Потому что каждое из множеств $F_1,\ldots, F_n$ содержит все $x_m$ для $m>n$.

Кстати, у Вас там путаница какая-то с $\Im$ и $\mathfrak{F}$. Не описано, что такое $M_n$. И зачем нужно какое-то $Y$, почему не сразу $M\subset X$?

[maxmatem]

ну это одно и тоже! да я забыл написать что $\[{M_n} = \{ {x_n},{x_{n + 1}},...\} \] $,