Даны две функции:
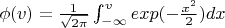
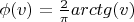
Необходимо обосновать, что они обе подходят под определение сигмоидной функции.
Более-менее определение нашел в
википедии:
Цитата:
For lack of complex descriptions a sigmoid function is often used. A sigmoid curve is produced by a mathematical function having an "S" shape.
...
In general, a sigmoid function is real-valued and differentiable, having either a non-negative or non-positive first derivative and exactly one inflection point. There are also a pair of horizontal asymptotes as
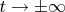
Как я понял, необходимо доказать, что данные функции дифференцируемы (найти предел?), первую производную и точку перегиба. Построить график для того, чтобы убедиться, что он S-образный, а так же найти горизонтальные асимптоты.
Правильно?



