Спасибо большое за подробные разъяснения и выкладки. Вы очень помогли понять что мне нужно)). Попробую сформулировать задачу теперь.
(я допустил ошибку при написании формулы прежде, прошу прощения, думаю она не повлияла на существо задачи)
Итак
Даны три последовательности:

. На этих трех последовательностях задана четвертая последовательность

определяемая рекуррентной формулой

.
Требуется преобразовать формулу так, чтобы

-й член последовательности

зависел лишь от соответствующих элементов последовательностей

, то есть

зависит от
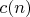
,

и

. Т. е. по существу найти нерекуррентную формулу

-го члена.
Или же представить формулу в виде ряда, члены которого обладают указанным свойством, т.е. зависят лишь от !соответствующих! элементов первых трех последовательностей.
Постановка не противоречива, что показывает, например, последовательность Фибоначчи или последовательность приближений числа pi.
Буду рад любым идеям, советам, критике.



