
Условие

Зачем оно?!
Интуиция подсказывает, что нужно решать с помощью замены

Но ничего путного оттуда не извлек((( (см пункт 2 и 3)
Решал так....
1)



(1)
a) Ищем общее решение однородного уравнения


b) Частное решение неоднородного ищем в виде

Подставляя

в (1) получаем

=>

;
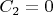
=>

c) Общее решение неоднородного уравнения

Тут условие

трудновато придумать как использовать!
2) Попробуем сделать замену


Уравнение примет вид
![$e^{6x}dx+[cos(6y)+xe^{6x}]\cdot 6dx=0$ $e^{6x}dx+[cos(6y)+xe^{6x}]\cdot 6dx=0$](https://dxdy-04.korotkov.co.uk/f/f/1/f/f1fbd80bdeea2b1c2d4531f8f6fd852f82.png)

Дальше что-то делать - нет смысла...
3) Сделаем замену

А то, что это равно 6, учтем потом, если дойдем до этого

Изначальное уравнение примет вид
![$e^{tx}dx+t(cos[tx]+xe^{tx})(tdx+xdt)=0$ $e^{tx}dx+t(cos[tx]+xe^{tx})(tdx+xdt)=0$](https://dxdy-02.korotkov.co.uk/f/d/3/3/d3306e4bc75f46b8da8810c58ce0fbb082.png)
![$(e^{tx}+tcos[tx]+txe^{tx})dx+(xcos[tx]+x^2e^{tx})dt=0$ $(e^{tx}+tcos[tx]+txe^{tx})dx+(xcos[tx]+x^2e^{tx})dt=0$](https://dxdy-01.korotkov.co.uk/f/c/a/d/cad693dedc0450515a2fac034c10f44882.png)
А что дальше делать - не понятно...



