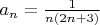Методом "расписывания" частичных сумм он не решается, т.е мы вынесем 2 , но в скобке получится ненатуральное число
Хорошая идея рассмотреть функцию вида

в единице значение совпадает с суммой нашего ряда
дифференцируем

, причесываем и заменяем

,таким образом

Обозначаем

, дифференцируем

, получаем прогрессию ,сумма равна

/ Затем интегрируем,

легко находится и равен

а вот дальше интеграл не очень-то берется, даже в предельном смысле!
http://integrals.wolfram.com/index.jsp Вольфрам берет его, но без модуля аргумента логарифма, и подстановки x=0,1 ничего не дают (ф-ия не существует)
Ваши предложения? ещё раз сформулирую задачу Найти сумму ряда с членом