Ну хотя бы это может как-то поможет:
Теоремы Силова-- Ср дек 23, 2009 14:36:18 --Если определение там правильно написано (то есть силовская подгруппа - это подгруппа степени

в

, причем

делит
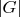
, но

не делит
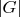
), то берем группы типа

порядка 2 и декартово их перемножаем (смотрим, чтобы все

были различны) - получим группу порядка 8. Только она не цикличная тогда... И образующие ее видны в таком виде тоже.
-- Ср дек 23, 2009 14:38:59 --Ага, еще можно пытаться брать

и тоже декартово перемножать - у них будут другие системы образующих...
-- Ср дек 23, 2009 14:40:42 --Ммм, и теперь, если не существует циклической подгруппы в

с образующей порядка 8 (вроде бы ее нет), то можно просто подсчитать все получающиеся вышеуказанные подгруппы...
-- Ср дек 23, 2009 14:42:41 --Что такое нормализатор, можно узнать здесь:
Словарь терминов теории групп-- Ср дек 23, 2009 14:53:33 --И еще: поскольку силовская группа нормальна, то она содержится в нормализаторе. Можно ее отсюда поискать (но если не хотите - не пробуйте, я сам не знаю, м.б. это сллишком долго).
Однако силовских подгрупп у нас до фига получилось, а нормализатор их все содержит! Значит нормализатор от

недалеко ушел, либо я что-то не то говорю...



