Решил написать решение п. 1.5.
Решение основано на оценках интерполяционных определителей из этой статьи.Лемма 1. Пусть

,

,

--- целая функция,

. Тогда справедливо неравенство

где обозначено


и постоянная

.
Док-во. Рассмотрим целую функцию

По принципу максимума,

Но при


поэтому

Наконец, по формуле Стирлинга,

Лемма доказана.

В следующей лемме используются те же обозначения.
Лемма 2. Пусть

--- целые функции,
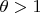
. Тогда справедливо неравенство

(

--- группа подстановок множества

).
Доказательство. Индукция по

.
Рассмотрим функцию

По лемме 1,

Разложим определитель по последнему столбцу:

Тогда

Оценивая

по индукционному предположению, получаем требуемое.

П. 1.5 задачи моментально следует из леммы 2, поскольку

(

).
P.S. На самом деле то, что значения функций рассматриваются в натуральных числах, здесь не совсем по существу (просто оценки получаются получше благодаря формуле Стирлинга). Так, можно доказать, что для произвольных целых функций

, произвольных комплексных чисел

, занумерованных в порядке возрастания модулей (т.е.

), и произвольных

справедливо неравенство

(Целость функций можно заменить на голоморность в круге

.)



