Это приводит к аксиомам кольца, поля или тела, из которых Ваши "операции с качествами" автоматически следуют.
Someone, я не знаю чем вас так греют эти аксиомы.
Это простые аксиомы. Основанные на них алгебраические системы имеют широчайшую область применения. Ваши "операции с качествами" автоматически следуют из этих аксиом, поэтому нет никакой нужды вводить эти "качества" и специальными аксиомами определять операции с ними.
Они явно не могут ответить на поднимаемые вопросы.
1. Покажите мне пожалуйста, где в аксиомах кольца/поля/тела говорится про операцию возведения в степень?
Нигде. В случае произвольного кольца/поля/тела "бинарная операция"

не является алгебраической операцией, хотя при определённых условиях можно ввести бесконечное множество унарных операций

,

,

,...
2. Покажите мне пожалуйста, как можно видеть различие между действительными и комплексными числами по аксиомам кольца/поля/тела?
Эти аксиомы служат не для того, чтобы различать кольца/тела/поля. Они устанавливают свойства алгебраических операций, общие для всех колец/полей/тел.
3. Можно ли по аксиомам кольца/поля/тела доказать(опровергнуть) возможность непротиворечивого введения операции возведения в степень для комплексных чисел?
Это зависит от того, что Вы понимаете под "операцией возведения в степень".
Из пунктов 1, 2 например следует, что упомянутые аксиомы не компетентны ответить на вопрос "Противоречит ли для комплексных чисел постулированный дистрибутивный закон

требованию

?".
4. Ответите на этот вопрос исходя из аксиом кольца/поля/тела? (Ответ будет "Нет").
Разумеется, отвечу: указанное свойство операции возведения в степень для целых действительных

и

не имеет никакого отношения к дистрибутивности умножения относительно сложения (в частности, никак не может ему противоречить) и следует из ассоциативности умножения в поле. Однако определение степени для нецелого показателя очень далеко выходит за рамки собственно алгебры, а соотношение

для комплексных

, вообще говоря, не выполняется (точнее, оно выполняется с такой оговоркой: для каждого значения

можно подобрать такие значения

и

, что равенство будет верным; дистрибутивность умножения относительно сложения здесь важна).
Операция возведения в степень вводится только через изменение набора аксиом, а это выводит нас за пределы аксиом колец/полей.
Ерунда. Возведение в степень вводится определением без какого-либо изменения набора аксиом.
Тогда почему эту Вашу гипотетическую операцию нужно называть возведением в степень?
По той же причине, по которой операции

называются операцией возведения в степень.
Уж извините, после этого я задумываюсь, что же называть "наивная кустарщина".
Ну разумеется, Вы же не знаете, что называется степенью элемента алгебраической системы. И это странно, потому что это изучают в школе (применительно к действительным числам). Поэтому Ваши измышления кажутся Вам необыкновенно глубокими.
Рассмотрим произвольный
группоид 
, то есть, множество с одной бинарной операцией, которую будем называть умножением; произведение элементов

и

будем обозначать

.
Вообще, если

- натуральное число, то
 -ной степенью элемента
-ной степенью элемента  называется произведение
называется произведение  одинаковых множителей, равных
одинаковых множителей, равных 
. В произвольном группоиде такое определение при

ничего конкретного не определяет, так как это произведение зависит от расстановки скобок в выражении

, например,

и

могут быть разными элементами.
Поэтому следует ограничиться группоидами, в которых при всех

произведение

одинаковых множителей не зависит от расстановки скобок. В таком группоиде

-ная степень элемента

обозначается

. Очевидным образом для любых

выполняются равенства

и

.
Если группоид имеет
единичный элемент, то есть, такой элемент

, что

и

для любого элемента

, то можно определить также
нулевую степень равенством

. Равенства

и

выполняются и для нулевой степени, то есть, когда

или

равно

. Равенство

тривиально.
Далее будем предполагать, что группоид

является
полугруппой, то есть, операция умножения удовлетворяет условию
ассоциативности:

для любых

.
Поскольку в полугруппе произведение любых (не только одинаковых) элементов не зависит от расстановки скобок, то в полугруппе можно определить степень

при

, а если существует единичный элемент

, то можно определить и

. Разумеется, равенства

и

в полугруппе выполняются. Если полугруппа коммутативная, то также

.
Если элемент полугруппы

имеет
обратный элемент, то есть, такой элемент

, что

и

, то можно определить отрицательную степень элемента

равенством

. Благодаря ассоциативности умножения равенства

и

будут выполняться для любых целых

. Если полугруппа коммутативная, то для

и обратимых

и

будет выполняться и равенство

.
В частности, в группе для всех элементов определены степени с любыми целыми показателями и выполняются указанные свойства степеней (равенство

- для коммутативной группы).
Поскольку умножение в теле и поле ассоциативно, то неотрицательные степени определены для всех элементов тела и поля (в частности,

; здесь только нужно помнить, что тот

, который в основании степени, и

- это элементы поля или тела, а тот

, который в показателе степени, - элемент множества целых чисел), а отрицательные - для ненулевых элементов.
В кольце степени элементов можно определить, если мультипликативный группоид кольца удовлетворяет перечисленным выше условиям. В частности, в ассоциативном кольце положительные степени элементов определены всегда, нулевая - в кольце с единицей, отрицательные - для обратимых элементов.
От привычных

придется отказаться, так как они навязывают законы

, которые не могут одновременно выполняться в группе. Но этот отказ не должен быть болезненным, если принять во внимание, что все эти равенства были введены "по определению" и кроме привычки в их защиту ничего нет.
Указанные Вами "привычные" равенства являются следствиями приведённого выше общего определения степени. Вы, конечно, можете выдумать что угодно и назвать это степенью, но при этом вступите в конфликт с общепринятой терминологией. Вы уверены, что Ваша выдумка будет иметь столь большой успех, что все срочно откажутся от общепринятой терминологии и от обычного понятия степени в пользу Вашего?
Продолжим.
Введение степеней с нецелыми показателями выходит за пределы собственно алгебры.
В частности, определение поля действительных чисел включает не только алгебраические операции с их аксиомами, но также отношение порядка с его аксиомами, аксиому полноты и аксиому Архимеда.
Пользуясь этими аксиомами, можно
1) для неотрицательного числа

и натурального

определить степень

как неотрицательное действительное число, удовлетворяющее условию

и доказать существование и единственность этого числа (после этого для нечётного

можно определить

и для отрицательных

равенством

), доказать монотонность

по

и по

, а также равенства

,

,

,

;
2) если определено

, то для неотрицательного

определить

; если

, то можно определить

и для отрицательного

; далее нужно доказать равенство

при

(это позволяет говорить о степени с рациональным показателем

), свойства

,

,

,

,

, а также монотонность

по

и по

;
3) "зажимая" действительное число

сходящимися к нему сверху и снизу последовательностями рациональных чисел, определить

для неотрицательного

, если
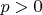
, и для положительного

, если

, и доказать свойства, аналогичные перечисленным в предыдущем пункте.
Для комплексных чисел

и

степень определяется равенством

. Из-за многозначности логарифма степень также оказывается многозначной. Единственность такого определения следует из единственности аналитических функций

и

, совпадающих с функциями

и

(для действительных

и

и комплексного

).