Массивные калибровочные поля и преобразования сдвига

[Утундрий]

Вы ее в состоянии от начала и до конца более-менее подробно здесь изложить? Без вот этого вот "на деревню дедушке":

Цитата:

лагранжиан стандартен, как в статье ЯМ

-- Ср сен 30, 2009 01:16:23 --

И еще вопрос. Насколько я понимаю, вы снова сделали тот же самый финт ушами, что и в примере с векторным полем. Какие у вас есть основания полагать, что то что не сработало в прошлый раз, вдруг заработает теперь? Я пока что вижу только глюоны, пусть и самодействующие, но в упор не наблюдаю того, что бы эти глюоны могли склеивать.

[ИгорЪ]

Утундрий в сообщении #247661 писал(а):

И еще вопрос. Насколько я понимаю, вы снова сделали тот же самый финт ушами, что и в примере с векторным полем. Какие у вас есть основания полагать, что то что не сработало в прошлый раз, вдруг заработает теперь? Я пока что вижу только глюоны, пусть и самодействующие, но в упор не наблюдаю того, что бы эти глюоны могли склеивать.

Завтра напишу, а это я не понял, чё за финт? что не сработало? какое векторное поле? Глюоны склеивают фермионные поля, за счет удлинения производной, а мы то пока в бозонном секторе, причем в безхиггсовом варианте.

[Утундрий]

Подождем до завтра, время терпит.

[Munin]

Хм. Я тут осознал, что замена переменных общего вида, пока мы изучаем лагранжиан, может быть допустима, но когда исследуем теорию на перенормируемость - может быть уже недопустима. Потому что пределы по старым переменным и по новым не совпадают. Так что, может быть, часть своих прежних слов беру назад. К замене переменных в теории поля надо подходить с большой осторожностью. К заменам в Хиггсе и ГВС это не относится, они там попросту линейные.

[ИгорЪ]

Для простоты пишу абелев вариант лагранжиана содержащего при разных температурах разные фазы. С групповой точки мы описываем разные фазы разными группами. Пример не очень характерен из-за локальной изоморфности групп, но зато прост. Более сложный вариант $SO(3) \to E(2)$ будет легче понять после этого. Итак, $L=R^{2Q(T-T_c)-2} ((\partial( R))^2+R^2(\partial \phi-A)^2 )- F^2 $, где $Q(x)=1$ при положительном $x$, и $Q(x)=0$ при отрицательном аргументе (ступенька одним словом, которую можно сгладить арктангенсом или ещё чемнить, дабы получить желаемую кинетику перехода из одной фазы в другую. У нас ноль величины $x=T-T_c$ разделяет две фазы. Высокотемпературная $Q=1$ - локализованные изовращения двухкомпонентного поля или безмассовая скалярная электродинамика в полярных координатах$(R, \phi)$ с калибровочными преобразованиями $\phi\to \phi+a(x)$, $R \to R$, $A \to A+\partial a$ и лагранжианом$L_1=(\partial( R))^2+R^2(\partial \phi-A)^2 - F^2 $
Низкотемпературная при $Q=0$ - локализованные преобразования галилея $\psi \to \psi+r a(x)$, $r \to r$, в изопространстве функций$(r,\psi)$, где$r=\ln(R)$ и $\psi=r\phi$ , c лагранжианом $L_0=(\partial( r))^2+(\partial \phi-A)^2 - F^2$, описывающим некий невзаимодействующий скаляр $r$ и массивное калибровочное поле.

[Munin]

Не врубаюсь, каким образом у вас температура аргументом лагранжиана стала.

[ИгорЪ]

$x$ это просто феноменологический параметр зависящий от температуры (или энергии), как $\alpha$ или $\beta$ здесь http://en.wikipedia.org/wiki/Ginzburg%E ... dau_theory

[Munin]

Так там и лагранжиан феноменологический, наверное, от температуры зависящий. А теоретический из него как построить?

[ИгорЪ]

Насколько мне известно, теория ГЛ описывает макроскопическую многочастичную волновую функцию, посему она изначально феноменологическая. Микроскопическое описание даёт теория БКШ, из которой статистическим гиббсовским усреднением можно получить свободную энергию ГЛ с нужными температурными зависимостями коэффициентов $\alpha, \beta$.

[ИгорЪ]

Попробую обновить тему, вдруг кто за это время подучился.
Речь о массе калибровочных полей, да и всех остальных. Общепринят механизм Хиггса. Предлагается альтернатива. Без специально подобранного потенциала и частиц Хиггса.

Введение.

Локализация глобальных фазовых преобразований$\phi\to e^a\phi, \partial\phi\to e^a\partial\phi$, достигается введения безмассового калибровочного поля $A$, с преобразованиями $\phi\to e^a(x)\phi, (\partial-A)\phi\to e^a(x)(\partial-A)\phi$, $A \to A+\partial a$. Это простейшая абелева теория есть всем известный электромагнетизм. Безмассовость следует из того, что массовый квадратичный по$A$ член не выдерживает этих преобразований. Хиггсов механизм придуман для придания массы калибровочным полям.
Рассмотрим абелев вариант механизма Хиггса. Калибровочно инвариантный лагранжиан для комплексного поля $\psi=R\exp(i\phi)$ в радиальных переменных выглядит
$L=(\partial( R))^2+R^2(\partial \phi-A)^2 - F^2 -V(R)$
$\phi\to \phi+a(x)$, $R \to R$, $A \to A+\partial a$
фиксируем калибровку $\phi=0$, тогда
$L=(\partial( R))^2+R^2 A^2 - F^2 -V(R)$ и далее сдвиг на минимум потенциала $R(x)=m+\chi(x)$дает массовый член и хиггсово поле. $F^2$ - лагранжиан электромагнитного поля. Потенциал специально подобран, чтобы иметь минимум не в нуле, а в $m$ . Вот и весь механизм.

Теперь наблюдение.

Примите $R=const$. Сдвиг делать не надо. Получите сразу массовый член. Без хиггсов и потенциала. Обратите внимание, что в полярных координатах фазовые преобразования выглядят как преобразования сдвига. Поэтому напрашивается

Общее наблюдение.

Локализация глобальных преобразований сдвига$\phi\to \phi+a, \partial\phi\to \partial(\phi+a)$, достигается введения безмассового калибровочного поля $A$, с обычными преобразованиями и странной "длинной " производной $\phi\to \phi+a(x), (\partial\phi-A) \to (\partial\phi-A)$, $A \to A+\partial a$. Кинетическое слагаемое лагранжиана$(\partial\phi-A)^2$ содержит массовый член для поля $A$. Итак, при локализации групповых преобразований содержащих сдвиги соответствующие поля массивны.

Фазовые переходы.

Можно сделать чтобы массивность приобреталась с понижением температуры. Итак, $L=R^{2Q(T-T_c)-2} ((\partial( R))^2+R^2(\partial \phi-A)^2 )- F^2 $, где $Q(x)=1$ при положительном $x$, и $Q(x)=0$ при отрицательном аргументе (ступенька одним словом, которую можно сгладить арктангенсом или ещё чемнить, дабы получить желаемую кинетику перехода из одной фазы в другую. У нас ноль величины $x=T-T_c$ разделяет две фазы. Высокотемпературная $Q=1$ - локализованные изовращения двухкомпонентного поля или безмассовая скалярная электродинамика в полярных координатах$(R, \phi)$ с калибровочными преобразованиями $\phi\to \phi+a(x)$, $R \to R$, $A \to A+\partial a$ и лагранжианом$L_1=(\partial( R))^2+R^2(\partial \phi-A)^2 - F^2 $
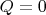
Низкотемпературная при $Q=0$ - локализованные преобразования галилея $\psi \to \psi+r a(x)$, $r \to r$, в изопространстве функций$(r,\psi)$, где$r=\ln(R)$ и $\psi=r\phi$ , c лагранжианом $L_0=(\partial( r))^2+(\partial \phi-A)^2 - F^2$, описывающим после фиксации калибровки $\phi=0$, некий невзаимодействующий скаляр $r$ и массивное калибровочное поле.

[Утундрий]

Помню, помню. Только мне нечего пока сказать.

[ИгорЪ]

Ну это очень хороший ответ.