Ну возьмем какое-нибудь поле

.
Рассмотрим какую-нибудь алгебру

над этим полем.
Возьмём какой-нибудь группоид

. Для примера множество натуральных чисел по сложению.
Пусть

Тогда если
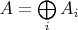
,
то

называется

-цветной алгеброй, а

её раскраской.
А что даёт вообще вся общая алгебра? Применяется где-то, работает...