Построение классической механики на кинематических принципах

[olav]

PapaKarlo в сообщении #238789 писал(а):

olav в сообщении #238708 писал(а):

Речь идет о математических принципах, а не о практике. На практике не бывает стопроцентно-инерциальной системы отсчета, точно также как не бывает треугольника, сумма углов которого в точности равна 180 градусам. Не надо путать метрологию с теоретической механикой.

Это Вы себе скажите. Задача, на которую я ссылаюсь, из учебника под названием... Вы в жизни не догадаетесь, под каким. Вот посмотрите задачку, найдете название учебника, а потом будете рассуждать о метрологии и пр.

olav в сообщении #238708 писал(а):

беретесь ли вы оспаривать справедливость кинематических принципов?

Да я уже высказал свое мнение. И Вы лишь подтвердили его: Ваш принцип №1, который говорит, что надо называть ИСО, Вы применить к простейшей задаче не можете. Заметьте, я не предлагаю Вам решить задачу. Я предложил лишь продемонстрировать на примере этой задачи применение одного из сформулированных Вами принципов. Если это возможно - продемонстрируйте. Если невозможно - грош цена Вашим кинематическим принципам.

Следующие вопросы - только после демонстрации.

Так че там в той задаче надо определять-то? Какая система отсчета инерциальная? Так та самая, в которой ускорение любой материальной точки в любой момент времени стремится к нулю при стремлении к бесконечности радиус-векторов всех остальных точек. В той задаче даже с условиями не определились: стрежень с пружинками и колечками там замкнутая система или он к стене прикреплен?

-- Пт авг 28, 2009 22:38:31 --

arseniiv в сообщении #238746 писал(а):

olav в сообщении #238708 писал(а):

точно также как не бывает треугольника, сумма углов которого в точности равна 180 градусам

А вот тут логическая ошибка.
Кстати, радиус-векторы точек должны отсчитываться от какого-то центра какой-то системы координат. У вас про оные ничего не сказано... Значит, даже математическая формулировка некорректна, вот так...

От центра координат системы отсчета, упомянутой в первом кинематическом принципе.

[PapaKarlo]

olav в сообщении #238802 писал(а):

Так че там в той задаче надо определять-то? Какая система отсчета инерциальная? Так та самая, в которой ускорение любой материальной точки в любой момент времени стремится к нулю при стремлении к бесконечности радиус-векторов всех остальных точек. В той задаче даже с условиями не определились: стрежень с пружинками и колечками там замкнутая система или он к стене прикреплен?

Будем считать, что Вы не поняли, что надо продемонстрировать, а также нуждаетесь в уточнении условия, поэтому я отвечу на Ваши вопросы. Пожалуйста:

1) Стержень прикреплен к стене. Вопросы про стену тоже последуют?

2) Что требовалось определить в той задаче, нас в этой теме не интересует. Интересует указанное в п.3:

3) Вопрос был не о том, какая система инерциальная (как найти инерциальную систему в условиях, указанных в задаче). Вопрос был о том, какова система отсчета, которая уже используется Геронимусом для решения задачи: инерциальная или неинерциальная. И обосновать ответ на этот вопрос Вам предлагается с использованием Вашей аксиоматики.

[Vallav]

Пружина - неправильное устройство.
Так как сила, с которой она действует, при удалении
точек на бесконечность не спадает до нуля ( естественно,
пока пружина остается пружиной ).
И закрепление стержня в стене - неправильное
устройство. Что в бесконечность удалять?
Но если поступить по Ньютону - рассмотреть в этой СО
пробное тело ( индикатор ) и посмотреть, как оно себя ведет -
вроде прокатывает.

[olav]

PapaKarlo в сообщении #238838 писал(а):

olav в сообщении #238802 писал(а):

Так че там в той задаче надо определять-то? Какая система отсчета инерциальная? Так та самая, в которой ускорение любой материальной точки в любой момент времени стремится к нулю при стремлении к бесконечности радиус-векторов всех остальных точек. В той задаче даже с условиями не определились: стрежень с пружинками и колечками там замкнутая система или он к стене прикреплен?

Будем считать, что Вы не поняли, что надо продемонстрировать, а также нуждаетесь в уточнении условия, поэтому я отвечу на Ваши вопросы. Пожалуйста:

1) Стержень прикреплен к стене. Вопросы про стену тоже последуют?

Ускорение стены в ИСО равно нулю? Если нет, то чему равно ускорение стены в ИСО?

Цитата:

2) Что требовалось определить в той задаче, нас в этой теме не интересует. Интересует указанное в п.3:

3) Вопрос был не о том, какая система инерциальная (как найти инерциальную систему в условиях, указанных в задаче). Вопрос был о том, какова система отсчета, которая уже используется Геронимусом для решения задачи: инерциальная или неинерциальная. И обосновать ответ на этот вопрос Вам предлагается с использованием Вашей аксиоматики.

Ну если по условию задачи стена неподвижна в какой-нибудь ИСО, а соответсвенно и стержень, к ней прикрепленный, то ответ содержится в условии задачи - система отсчета, связанная со стержнем инерциальная, и привлекать мою аксиоматику к получению ответа, который уже содержится в условиях задачи, мягко говоря, нет необходимости.
А вообще вы даже не обратили внимания на то, что все уравнения динамики при применении кинематического подхода к изложению классической механики становятся следствиями четырех кинематических принципов. Поэтому для решения задач можно использовать те же самые уравнения динамики, которые используете вы, помня при этом, что они являтся следствиями кинематических принципов. У вас буквами F и m обозначены первичные сущности, которым не дается определения, у меня же им дается математическое определение, т.е. F и m это не более чем вспомогательные обозначения для неких кинематических величин - и в уравнениях, их содержащих, всегда можно сделать подстановку того, обозначением чего они являются.

-- Сб авг 29, 2009 16:50:02 --

Vallav в сообщении #238918 писал(а):

Пружина - неправильное устройство.
Так как сила, с которой она действует, при удалении
точек на бесконечность не спадает до нуля ( естественно,
пока пружина остается пружиной ).
И закрепление стержня в стене - неправильное
устройство. Что в бесконечность удалять?

Вы до сих пор не можете понять, что никто точки на бесконечность не удаляет. Речь идет о пределе функции нескольких аргументов при стремлении некоторых аргументов к бесконечности. Надеюсь, что такое предел функции вы знаете? И разницу между удалением точек на бесконечность и стремлением функции нескольких аргументов к пределу при стремлении некоторых аргументов к бесконечности понимаете?

Цитата:

Но если поступить по Ньютону - рассмотреть в этой СО
пробное тело ( индикатор ) и посмотреть, как оно себя ведет -
вроде прокатывает.

[PapaKarlo]

olav в сообщении #238947 писал(а):

Ускорение стены в ИСО равно нулю? Если нет, то чему равно ускорение стены в ИСО?

Я так и предполагал - вопросы последовали. Но теперь уж извините - мой ответ после Вашего. Тем более, что цель моего вопроса как раз в том и заключается, чтобы Вы ответили, как можно решить, является ли некая СО инерциальной - применительно к указанной задаче. Как из Вашей аксиоматики определить ускорение стены и т.д. Пожалуйста, не уклоняйтесь от ответа.

olav в сообщении #238947 писал(а):

Ну если по условию задачи стена неподвижна в какой-нибудь ИСО, а соответсвенно и стержень, к ней прикрепленный, то ответ содержится в условии задачи - система отсчета, связанная со стержнем инерциальная, и привлекать мою аксиоматику к получению ответа, который уже содержится в условиях задачи, мягко говоря, нет необходимости.

Мягко говоря, и в других случаях - ИМХО тоже нет необходимости. Но меня интересует не столько необходимость, сколько возможность привлечения и демонстрация этого привлечения на примере указанной задачи.

Можете считать, что стена в какой-нибудь ИСО неподвижна. Но точек вблизи конца стержня - как собак нерезанных. Как применить Вашу аксиому №1? Как посчитать предел функции? Пожалуйста - грубо, весомо, зримо.

Если же наличие ИСО снимает, как Вы говорите, необходимость и возможность привлечения Вашей аксиоматики, считайте, что про стену нам ничего не известно. Но вопрос об инерциальности СО, связанной с концом закрепленного в стене стержня остается животрепещущий. И кроме Вашей аксиоматики другой нет. Как быть? Продемонстрируйте.

[ewert]

olav в сообщении #238947 писал(а):

Вы до сих пор не можете понять, что никто точки на бесконечность не удаляет. Речь идет о пределе функции нескольких аргументов при стремлении некоторых аргументов к бесконечности.

Что ровно и означает удаление точек на бесконечность.

[olav]

PapaKarlo в сообщении #238966 писал(а):

olav в сообщении #238947 писал(а):

Ускорение стены в ИСО равно нулю? Если нет, то чему равно ускорение стены в ИСО?

Я так и предполагал - вопросы последовали. Но теперь уж извините - мой ответ после Вашего. Тем более, что цель моего вопроса как раз в том и заключается, чтобы Вы ответили, как можно решить, является ли некая СО инерциальной - применительно к указанной задаче. Как из Вашей аксиоматики определить ускорение стены и т.д. Пожалуйста, не уклоняйтесь от ответа.

А зачем тогда вообще стена понадобилась в условии задачи, если надо определять ее ускорение. Если надо определять ее ускорение, то стена тогда является просто как бы продолжением стержня и надо тогда рассматривать замкнутую систему из стены и стержня с пружинами и колечками. Не проще ли тогда обойтись без стены и рассматривать замкнутую систему из стержня с пружинами и колечками?

Цитата:

olav в сообщении #238947 писал(а):

Ну если по условию задачи стена неподвижна в какой-нибудь ИСО, а соответсвенно и стержень, к ней прикрепленный, то ответ содержится в условии задачи - система отсчета, связанная со стержнем инерциальная, и привлекать мою аксиоматику к получению ответа, который уже содержится в условиях задачи, мягко говоря, нет необходимости.

Мягко говоря, и в других случаях - ИМХО тоже нет необходимости. Но меня интересует не столько необходимость, сколько возможность привлечения и демонстрация этого привлечения на примере указанной задачи.
Можете считать, что стена в какой-нибудь ИСО неподвижна.

Давайте лучше считать, что стены нет вообще. Она только мешает рассуждениям.

Цитата:

Но точек вблизи конца стержня - как собак нерезанных. Как применить Вашу аксиому №1? Как посчитать предел функции? Пожалуйста - грубо, весомо, зримо.

Так пределы функции не надо считать, потому что их отношение задано в задаче. Допустим в задаче заданы динамические массы $m_1=5$кг, $m_2=2$кг.
Введем обозначение для безразмерной кинематической массы.
$m_i\equiv 5\frac{a_{1i}}{a_{i1}}$. Получаем $5\frac{a_{11}}{a_{11}}=5$, $5\frac{a_{12}}{a_{21}}=2$,
$\frac{a_{12}}{a_{21}}=\frac{2}{5}$, где $a_{12}$ - модуль предела, к которому стремится ускорение материальной точки $1$ при стремлении к бесконечности радиус-векторов всех материальных точек замкнутой системы "стержень с пружинами и колечками", кроме точек $1$ и $2$, $a_{21}$ - модуль предела, к которому стремится ускорение материальной точки $2$ при стремлении к бесконечности радиус-векторов всех материальных точек замкнутой системы "стержень с пружинами и колечками", кроме точек $2$ и $1$. Как видим отношение пределов функции задано в задаче. ИСО будет та система, в которой все четыре кинематических принципа, дополненные выражением для кинематической силы $ F_i=-c\Delta x$, и их следствие - дифференциальное уравнение, фигурирующее в задаче Геронимуса, справедливы. Что такое кинематическая сила смотрите в файле. Таким образом, если в системе отсчета, связанной со стрежнем, данное дифференциальное уравнение справделиво, то система отсчета, связанная со стержнем - инерциальная.

Цитата:

Если же наличие ИСО снимает, как Вы говорите, необходимость и возможность привлечения Вашей аксиоматики, считайте, что про стену нам ничего не известно. Но вопрос об инерциальности СО, связанной с концом закрепленного в стене стержня остается животрепещущий. И кроме Вашей аксиоматики другой нет. Как быть? Продемонстрируйте.

[ewert]

olav в сообщении #238983 писал(а):

Давайте лучше считать, что стены нет вообще. Она только мешает рассуждениям.

Не дадим. А вдруг она есть?... Ведь это физически наблюдаемый факт. И куда Вы его приткнёте своими частицами?

[olav]

ewert в сообщении #238984 писал(а):

olav в сообщении #238983 писал(а):

Давайте лучше считать, что стены нет вообще. Она только мешает рассуждениям.

Не дадим. А вдруг она есть?... Ведь это физически наблюдаемый факт. И куда Вы его приткнёте своими частицами?

Если стена есть, то $a_{12}$ - модуль предела, к которому стремится ускорение материальной точки $1$ при стремлении к бесконечности радиус-векторов всех материальных точек замкнутой системы "стена со стержнем с пружинами и колечками", кроме точек $1$ и $2$, $a_{21}$ - модуль предела, к которому стремится ускорение материальной точки $2$ при стремлении к бесконечности радиус-векторов всех материальных точек замкнутой системы "стена со стержнем с пружинами и колечками", кроме точек $2$ и $1$

-- Сб авг 29, 2009 21:55:01 --

ewert в сообщении #238971 писал(а):

olav в сообщении #238947 писал(а):

Вы до сих пор не можете понять, что никто точки на бесконечность не удаляет. Речь идет о пределе функции нескольких аргументов при стремлении некоторых аргументов к бесконечности.

Что ровно и означает удаление точек на бесконечность.

Это вам так только кажется, потому что вы давно не освежали в памяти определение предела функции при стремлении аргументов к бесконечности.

[ewert]

olav в сообщении #238987 писал(а):

модуль передела

Достаточно, модулей переделов не бывает.

olav в сообщении #238987 писал(а):

ewert в сообщении #238971 писал(а):

olav в сообщении #238947 писал(а):

Вы до сих пор не можете понять, что никто точки на бесконечность не удаляет. Речь идет о пределе функции нескольких аргументов при стремлении некоторых аргументов к бесконечности.

Что ровно и означает удаление точек на бесконечность.

Это вам так только кажется, потому что вы давно не освежали в памяти определение предела функции при стремлении аргументов к бесконечности.

Поаккуратнее сударь. Вы одновременно и утверждаете уход точек на бесконечность, и отрицаете его. Шуточко -- грубовата, Вам никто не поверит.

[olav]

Если это был намек, чтобы я исправил опечатку, то, спасибо, я ее исправлю. А модуль предела бывает? Где я утверждаю уход точек на бесконечность? Возьмем к примеру первый кинематический принцип: существуют системы отсчета, в которых ускорение любой точки В ЛЮБОЙ МОМЕНТ ВРЕМЕНИ стремится к нулю при стремлении радиус-векторов всех остальных точек к бесконечности. Обратите внимание на слова, выделенные заглавными буквами. По-вашему в этом утверждении присутствуют бесконечные радиус-векторы? Нет речь всего навсего идет о пределе функции. Учите определение предела функции.

[PapaKarlo]

olav в сообщении #238802 писал(а):

В той задаче даже с условиями не определились: стрежень с пружинками и колечками там замкнутая система или он к стене прикреплен?

olav в сообщении #238983 писал(а):

А зачем тогда вообще стена понадобилась в условии задачи,

olav в сообщении #238983 писал(а):

Давайте лучше считать, что стены нет вообще. Она только мешает рассуждениям.

Вы дурака валяете? Другого ничего не остается, что ли? Кто здесь про стену начал разговор? Вы. А теперь скрипач не нужен? Вы уж определитесь.

olav в сообщении #238983 писал(а):

Так пределы функции не надо считать, потому что их отношение задано в задаче.

Цитату, пожалуйста. Дословно.

olav в сообщении #238983 писал(а):

Введем обозначение для безразмерной кинематической массы...

и далее. От того, что Вы ввели какие-то обозначения, еще не следует, что обозначенные величины имеют именно те значения, о которых Вы говорите. Докажите Ваше утверждение о значении пределов.

olav в сообщении #238983 писал(а):

Получаем $5\frac{a_{11}}{a_{11}}=5$, $5\frac{a_{12}}{a_{21}}=2$,
$\frac{a_{12}}{a_{21}}=\frac{2}{5}$

Первое равенство особо ценно , хотя оно не всегда имеет смысл. Кстати, что же такое $a_{11}$? Неужели это "модуль вектора $\vec a_{ii}$ - предела, к которому стремится в инерциальной системе отсчета модуль вектора ускорения точки $i$ $\vec a_i$ при стремлении к бесконечности радиус-векторов всех точек кроме точки $i$"? Если да, то чему же равно $a_{ii}$ в таких условиях?

Второе уравнение (равенство) нуждается в доказательстве.

olav в сообщении #238983 писал(а):

Как видим отношение пределов функции задано в задаче.

А зачем нам отношение пределов? Принцип 1 не упоминает никакого отношения пределов, но тем не менее описывает ИСО. Меня интересует лишь проверка, является ли некая СО инерциальной или нет - с помощью принципа, понятие ИСО описывающее.

olav в сообщении #238983 писал(а):

ИСО будет та система, в которой ...

Меня не интересует нахождение инерциальной СО. Я задал вопрос четко и недвусмысленно: является ли СО, связанная с концом стержня, инерциальной.

olav в сообщении #238983 писал(а):

ИСО будет та система, в которой все четыре кинематических принципа, дополненные выражением для кинематической силы $ F_i=-c\Delta x$, и их следствие - дифференциальное уравнение, фигурирующее в задаче Геронимуса, справедливы.

Принципы 2-4 опираются на понятие ИСО, используют его. ИСО определена в первом принципе, что подтверждается словами

olav в сообщении #237969 писал(а):

Назовем такие системы отсчета инерциальными.

Поэтому "...в которой все четыре кинематических принципа... справедливы" противоречит первому принципу. Не говоря уже о том, что Вам оказалось недостаточно не только четырех принципов и дополнения их выражением некоей силы - Вы еще потребовали выполнения некоего дифференциального уравнения, взятого из учебника Геронимуса. Последнее-то зачем? А если просто ограничиться частью условия задачи: "рассмотрим СО, связанную с концом $O$ неподвижного стержня, по которому скользят два колечка, кольца связаны пружинами...", и все, никаких вопросов о нахождении уравенения движения - что тогда скажет Ваша аксиоматика об инерциальности упомянутой СО. Ведь только это меня и интересует, а задача приведена лишь как пример, где рассматривается система отсчета.

Так что Ваше рассуждение не только не доказательно, но и просто странно, мягко говоря.

olav в сообщении #238983 писал(а):

Таким образом, если в системе отсчета, связанной со стрежнем, данное дифференциальное уравнение справделиво, то система отсчета, связанная со стержнем - инерциальная.

Нет, так мы не договаривались. Что же получается - Ваша аксиоматика неполна, требует еще и справедливости дифференциального уравнения, составленного Геронимусом?

Незачет. Вы не смогли показать, что Ваша аксиоматика позволяет сделать заключение по определению, которое якобы вводит Ваш первый принцип. Даже если привлечь три остальных и таинственную кинематическую силу - все равно аксиоматика якобы оказывается полной только после привлечения уравнения из задачки Геронимуса.

Работайте дальше над достижением полноты аксиоматики. Для начала удалите из Ваших рассуждений элементарные математические и логические ошибки. Неплохо бы немного физики добавить. Глядишь, суп из топора удастся.

Доработаете - милости просим.

[Vallav]

olav в сообщении #238947 писал(а):

Vallav в сообщении #238918 писал(а):

Пружина - неправильное устройство.
Так как сила, с которой она действует, при удалении
точек на бесконечность не спадает до нуля ( естественно,
пока пружина остается пружиной ).
И закрепление стержня в стене - неправильное
устройство. Что в бесконечность удалять?

Вы до сих пор не можете понять, что никто точки на бесконечность не удаляет. Речь идет о пределе функции нескольких аргументов при стремлении некоторых аргументов к бесконечности. Надеюсь, что такое предел функции вы знаете? И разницу между удалением точек на бесконечность и стремлением функции нескольких аргументов к пределу при стремлении некоторых аргументов к бесконечности понимаете?

Напомните, чему равен предел функции в случае двух
точек, соединенных пружиной. Когда один из аргументов
стремится к бесконечности.
Вариант - пружина порвется - не принимается.
У нас же предел функции...

И второе - пусть у нас три точки.
Ускорение первой точки можно представить в виде:
$a_1=a_1_1+a_1_2+a_1_3+a_1_2_3$
$a_1_1$ равно нулю, если СО - ИСО.
Как устанавливается, что при конечных аргументах
$a_1_2_3$
равен нулю, если этот член зануляется как при стремлении
аргументов точки 2 в бесконечность, так и при стремлении
аргументов точки 3 в бесконечность?
То есть, как у Вас постулируется отсутствие перекрестных
членов?

[ewert]

olav в сообщении #239005 писал(а):

Где я утверждаю уход точек на бесконечность?

Вот ровно тут:

olav в сообщении #239005 писал(а):

Возьмем к примеру первый кинематический принцип: существуют системы отсчета, в которых ускорение любой точки В ЛЮБОЙ МОМЕНТ ВРЕМЕНИ стремится к нулю при стремлении радиус-векторов всех остальных точек к бесконечности.

В частности. И вообще везде.

[olav]

PapaKarlo в сообщении #239057 писал(а):

olav всообщении #238802 писал(а):

В той задаче даже с условиями не определились: стрежень с пружинками и колечками там замкнутая система или он к стене прикреплен?

olav в сообщении #238983 писал(а):

А зачем тогда вообще стена понадобилась в условии задачи,

olav в сообщении #238983 писал(а):

Давайте лучше считать, что стены нет вообще. Она только мешает рассуждениям.

Вы дурака валяете? Другого ничего не остается, что ли? Кто здесь про стену начал разговор? Вы. А теперь скрипач не нужен? Вы уж определитесь.

Я спросил всего лишь, система, рассматриваемая в задаче Геронимуса, замкнута или нет. Обычно, если система незамкнута и прикреплена к стене, то стена считается неподвижной в ИСО. Поэтому я и спросил стена у вас в ИСО по условию задачи имеет нулевое ускорение или нет? Когда вы сказали, что нет, стало ясно, что стена для рассуждений не нужна, потому что вместо замкнутой системы "стержень, пружины, колечки" нужно опять же рассматривать замкнутую систему "стена, стержень, пружины, колечки". Хотя, если вы настаиваете на стене, то, действительно, можно рассматривать замкнутую систему "стена, стержень, пружины, колечки", но на ход рассуждений это никак не повлияет.

Цитата:

olav в сообщении #238983 писал(а):

Так пределы функции не надо считать, потому что их отношение задано в задаче.

Цитату, пожалуйста. Дословно.

Это не сказано прямым текстом в условиях задачи, тем не менее это должно быть для вас очевидным. У вас механика строится на динамических принципах, массы, заданные в условии задачи, размерны, и из второго и третьего законов Ньютона следует $\frac {m_2}{m_1}=\frac{a_{12}}{a_{21}}$, где $a_{1i}$ - модуль ускорения, которое получает точка $1$ под действием точки $i$, или модуль предела, к которому стремится ускорение точки $1$ при стремлении к бесконечности радиус-векторов всех точек замкнутой системы "стена, стержень, пружины, колечки", кроме точек $1$ и $i$. Так задано отношение модулей пределов ускорений в условиях задачи или нет?

Цитата:

olav в сообщении #238983 писал(а):

Введем обозначение для безразмерной кинематической массы...

и далее. От того, что Вы ввели какие-то обозначения, еще не следует, что обозначенные величины имеют именно те значения, о которых Вы говорите. Докажите Ваше утверждение о значении пределов.

Я ввожу обозначение таким образом, чтобы обозначенные величины имели именно те значения, которые у вас заданы в условииях задачи.
Далее, чтобы вы не путали кинематическую массу с динамической, кинематическую массу я буду обозначать штрихованной буквой. Как вы далее увидите, моя кинематическая масса отличается от вашей динамической только размерностью, но не численным значением, кинематическая масса - безразмерна, динамическая - размерна.
Введем обозначение $m_i'\equiv \frac {a_{1i}}{a_{i1}}m_1$, в этом математическом определении под $m_1$ понимается численное значение динамической массы, фигурирующей в задаче Геронимуса.
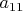
Получаем $m_1'\equiv \frac {a_{11}}{a_{11}}m_1=\frac {1}{1}m_1=1m_1=m_1$, $m_2'\equiv \frac {a_{12}}{a_{21}}m_1=m_2$, где $a_{11}$ - диагональный элемент матрицы для замкнутой системы материальных точек, диагональные элементы которой - безразмерные единицы, а недиагональные - модули пределов ускорений $a_{ik}$.
Как видим, $m_1'=m_1$, $m_2'=m_2$

Цитата:

olav в сообщении #238983 писал(а):

Получаем $5\frac{a_{11}}{a_{11}}=5$, $5\frac{a_{12}}{a_{21}}=2$,
$\frac{a_{12}}{a_{21}}=\frac{2}{5}$

Первое равенство особо ценно , хотя оно не всегда имеет смысл.

Первое равенство означет, что кинематическая масса $m_1'$ равна 5, $m_1'\equiv 5\frac{a_{11}}{a_{11}}=5$

Цитата:

Кстати, что же такое $a_{11}$? Неужели это "модуль вектора $\vec a_{ii}$ - предела, к которому стремится в инерциальной системе отсчета модуль вектора ускорения точки $i$ $\vec a_i$ при стремлении к бесконечности радиус-векторов всех точек кроме точки $i$"? Если да, то чему же равно $a_{ii}$ в таких условиях?

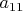
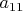
Конечно же, нет. Вы файл читали? $a_{11}$ - это диагональный элемент матрицы для замкнутой системы материальных точек, диагональные элементы которой - безразмерные единицы, а не диагональные - модули пределов ускорений $a_{ik}$. $a_{11}$ равен безразмерной единице.

Цитата:

Второе уравнение (равенство) нуждается в доказательстве.

Доказательство очень простое. Уже было доказано, что динамические уравения являются следствием кинематических принципов. Поэтому поскольку $F_{12}'=F_{21}'$, $F_{12}'=m_1'a_{12}, $F_{21}'=m_2'a_{21}$, то получаем $\frac {a_{12}}{a_{21}}=\frac {m_2'}{m_1'}$. Поскольку математическое определение для кинематической массы было выбрано так, чтобы численные значения кинематической массы совпадали с численными значениями динамических масс, фигурирующих в задаче, то $\frac {a_{12}}{a_{21}}=\frac {m_2}{m_1}$

Цитата:

olav в сообщении #238983 писал(а):

Как видим отношение пределов функции задано в задаче.

А зачем нам отношение пределов?

Я не знаю зачем оно вам, но это отношение пределов задано в условиях задачи.

Цитата:

Принцип 1 не упоминает никакого отношения пределов, но тем не менее описывает ИСО. Меня интересует лишь проверка, является ли некая СО инерциальной или нет - с помощью принципа, понятие ИСО описывающее.

Надеюсь, мне будет нетрудно ответить на этот вопрос после того как вы ответите на аналогичный вопрос. Ваш первый динамический принцип не упоминает никаких масс, но тем не менее описывает ИСО. Меня интересует лишь проверка, является ли некая СО инерциальной или нет - с помощью вашего первого динамического принципа, понятие ИСО описывающего. Напомню, что ваш первый динамический принцип гласит: существуют системы отсчета, в которых любая свободная материальная точка имеет нулевое ускорение.

Цитата:

olav в сообщении #238983 писал(а):

ИСО будет та система, в которой ...

Меня не интересует нахождение инерциальной СО. Я задал вопрос четко и недвусмысленно: является ли СО, связанная с концом стержня, инерциальной.

Меня тоже не интересует нахождение инерциальной СО. Я задал вопрос четко и недвусмысленно: является ли СО, связанная с концом стержня, инерциальной. Для ответа на этот вопрос вы должны воспользоваться вашим первым динамическим принципом, гласящим: существуют системы отсчета, в которых любая свободная материальная точка имеет нулевое ускорение, такие системы отсчета называются инерциальными.

Цитата:

olav в сообщении #238983 писал(а):

ИСО будет та система, в которой все четыре кинематических принципа, дополненные выражением для кинематической силы $ F_i=-c\Delta x$, и их следствие - дифференциальное уравнение, фигурирующее в задаче Геронимуса, справедливы.

Принципы 2-4 опираются на понятие ИСО, используют его. ИСО определена в первом принципе, что подтверждается словами

olav в сообщении #237969 писал(а):

Назовем такие системы отсчета инерциальными.

Поэтому "...в которой все четыре кинематических принципа... справедливы"
противоречит первому принципу.

Я чего-то никакого противоречия здесь не увидел. Если второй, третий и четвертый принцип справделивы в системах отсчета, упомянутых в первом принципе и названных инерциальными, то системы отсчета, упомянутые в первом, втором, третьем и четвертом принципе являются инерциальными.

Цитата:

Не говоря уже о том, что Вам оказалось недостаточно не только четырех принципов и дополнения их выражением некоей силы - Вы еще потребовали выполнения некоего дифференциального уравнения, взятого из учебника Геронимуса. Последнее-то зачем?

Для вас откровение, что для решения основной задачи механики - определения движения точек недостаточно одних только четырех динамических принципов (три закона Ньютона плюс принцип суперпозиции для силы) , и что их надо дополнять выражением для силы? Если же строить механику на кинематических принципах, то аналогично, для определения движения точек недостаточно одних только четырех кинематических принципов, их надо дополнять выражением для кинематической силы.
А уравнение, взятое из учебника Геронимуса, является следствием четырех кинематических принципов и выражения для кинематической силы. Подчеркиваю - следствием!

Цитата:

А если просто ограничиться частью условия задачи: "рассмотрим СО, связанную с концом $O$ неподвижного стержня, по которому скользят два колечка, кольца связаны пружинами...", и все, никаких вопросов о нахождении уравенения движения - что тогда скажет Ваша аксиоматика об инерциальности упомянутой СО. Ведь только это меня и интересует, а задача приведена лишь как пример, где рассматривается система отсчета.

И что тогда скажет ваша аксиоматика об инерциальности упомянутой СО? Еще раз напомню, что ваша аксиоматика гласит: существуют системы отсчета, в которых любая свободная точка имеет нулевое ускорение, такие системы отсчета называются инерциальными.

Цитата:

Так что Ваше рассуждение не только не доказательно, но и просто странно, мягко говоря.

Что тут странного? Я вам вначале показал, как кинематические соотношения следуют из динамических соотношений, если принять динамические соотношения за постулаты. Потом показал, как динамические соотношения следуют из кинематичесих соотношений, если принять кинематические соотношения за постулаты. Таким образом, механику можно строить либо на динамических постулатах, либо на кинематических постулатах. Если строить на кинематических, то на две первичные сущности будет меньше, потому что масса и сила в кинематических постулатах не фигурирует.

Цитата:

olav в сообщении #238983 писал(а):

Таким образом, если в системе отсчета, связанной со стрежнем, данное дифференциальное уравнение справделиво, то система отсчета, связанная со стержнем - инерциальная.

Нет, так мы не договаривались. Что же получается - Ваша аксиоматика неполна, требует еще и справедливости дифференциального уравнения, составленного Геронимусом?

Еще раз повторяю, дифференциальное уравнение, состтавленное Геронимусом является следствием четырех кинематических принципов и выражения для кинематической силы $F'=-c'\Delta x$

Цитата:

Незачет. Вы не смогли показать, что Ваша аксиоматика позволяет сделать заключение по определению, которое якобы вводит Ваш первый принцип.

Вы пока тоже не смогли показать, что Ваша аксиоматика позволяет сделать заключение по определению, которое якобы вводит Ваш первый динамический принцип. Значит тоже незачет?

Цитата:

Даже если привлечь три остальных и таинственную кинематическую силу - все равно аксиоматика якобы оказывается полной только после привлечения уравнения из задачки Геронимуса.

Уравнение из задачки Геронимуса - следствие из аксиоматики и выражения для кинематической силы

Цитата:

Работайте дальше над достижением полноты аксиоматики. Для начала удалите из Ваших рассуждений элементарные математические и логические ошибки.

Хотя бы одну математическую или логическую ошибку укажите, прежде чем давать такие советы

Цитата:

Неплохо бы немного физики добавить. Глядишь, суп из топора удастся.

А кинематика это по-вашему не физика?

Цитата:

Доработаете - милости просим.