| Заслуженный участник |
 |
09/05/08
1155
Новосибирск
|
В рамках обсуждения темы « Полное решение континуум-проблемы» возникло пожелание увидеть достаточно строгое и подробное доказательство (в ZFC) теоремы Цермело о вполне упорядочении. Откликаясь на это пожелание, ваш покорный сочинил один из возможных вариантов такого доказательства. Следует отметить, что при этом ничего нового изобретено не было. Это всего лишь слегка осовремененное и чуть-чуть оптимизированное доказательство, изложенное в монографии П.С.Александрова «Введение в теорию множеств и общую топологию» (глава 3, §5). Текст доказательства можно скачать в виде PDF-файла. По традиции этот текст дублирован ниже в теле сообщения. Итак... Теорема ЦермелоЛюбое множество может быть вполне упорядоченоПодробное доказательство в ZFCПусть  — произвольное непустое множество. По аксиоме выбора существует такая функция  , что  для всех для всех  . . Для  положим  . Заметим, что  . Для  положим  . Введем обозначение  для отношения сравнимости:  или  . Лемма 1. Пусть  , ,  , ,  . Тогда . Тогда  . .Итак, пусть  и и  . .
Наша цель — показать, что  . .
Если  , то , то  . .
Если  , то , то  . .
Пусть теперь  и и  . .
Поскольку  и и  , мы имеем , мы имеем  . .
Поскольку  и и  , мы имеем , мы имеем  . .
Следовательно,  , а значит, , а значит,  . . Положим  . Заметим, что  , так как, например,  . Положим  . Как легко видеть,  . Иными словами,  . Следовательно,  — наименьший по включению элемент  , т.е.  . Для  обозначим через ![$[x]$ $[x]$](https://dxdy-04.korotkov.co.uk/f/7/e/1/7e1c4a3a07c941625c2f20c594cb9f7c82.png) множество всех элементов  , сравнимых с  , т.е. положим ![$[x]:=\{y\in S : x\,{\raise.75pt\hbox{$\subset$}\mskip-10mu\lower.75pt\hbox{$\supset$}}\,y\}$ $[x]:=\{y\in S : x\,{\raise.75pt\hbox{$\subset$}\mskip-10mu\lower.75pt\hbox{$\supset$}}\,y\}$](https://dxdy-02.korotkov.co.uk/f/d/e/7/de713c20d76cd2022c9466cc824ecc7a82.png) . . Для  обозначим через ![$[X]$ $[X]$](https://dxdy-03.korotkov.co.uk/f/e/9/b/e9b9138812886eb81cff48ae91d583eb82.png) множество всех элементов  , сравнимых со всеми элементами  , т.е. положим , т.е. положим ![$[X]\,:=\,\bigcap_{x\in X}[x]\,=\,\bigl\{y\in S : (\forall\,x\in X)(x\,{\raise.75pt\hbox{$\subset$}\mskip-10mu\lower.75pt\hbox{$\supset$}}\,y)\bigr\}\,=\,\{y\in S : X\subseteq [y]\}$ $[X]\,:=\,\bigcap_{x\in X}[x]\,=\,\bigl\{y\in S : (\forall\,x\in X)(x\,{\raise.75pt\hbox{$\subset$}\mskip-10mu\lower.75pt\hbox{$\supset$}}\,y)\bigr\}\,=\,\{y\in S : X\subseteq [y]\}$](https://dxdy-03.korotkov.co.uk/f/2/9/f/29f67b4ab1eef318b038f675516d289382.png) . .
Отметим, что ![$[x]=[\{x\}]$ $[x]=[\{x\}]$](https://dxdy-02.korotkov.co.uk/f/d/8/5/d85fac52b44978a7f353c705aeb4b28a82.png) для всякого  . Лемма 2. Пусть  и и ![$Y\subseteq [X]$ $Y\subseteq [X]$](https://dxdy-01.korotkov.co.uk/f/8/a/1/8a18ef6c7ce114476b65780fcf1a871d82.png) . Тогда . Тогда ![${\cup}Y\in [X]$ ${\cup}Y\in [X]$](https://dxdy-02.korotkov.co.uk/f/d/b/b/dbb97a9cadbb2e7334dfc2ef1556c34682.png) . .Положим  и покажем, что и покажем, что ![$\bar y\in [X]$ $\bar y\in [X]$](https://dxdy-03.korotkov.co.uk/f/6/b/a/6bab49f7ef52aa7d7a5dd767020d9d3b82.png) . .
Поскольку ![$Y\subseteq [X]\subseteq S$ $Y\subseteq [X]\subseteq S$](https://dxdy-03.korotkov.co.uk/f/6/b/0/6b0e700356185a4581b7e47d4256707382.png) , мы имеем , мы имеем  , т.е. , т.е.  . .
Пусть  . Покажем, что . Покажем, что ![$\bar y\in [x]$ $\bar y\in [x]$](https://dxdy-02.korotkov.co.uk/f/d/1/d/d1df3e026f8d61385773308e0e543e7f82.png) , т.е. , т.е.  . .
Поскольку ![$Y\subseteq [X]\subseteq [x]$ $Y\subseteq [X]\subseteq [x]$](https://dxdy-02.korotkov.co.uk/f/5/9/c/59c7afdf39d71cbd5dda3172ede2cf6482.png) , мы имеем , мы имеем  для всех для всех  . .
Если  для всех для всех  , то , то 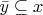 . .
Если же  для некоторого для некоторого  , то , то  , а значит, , а значит,  . . Лемма 3. Пусть ![$x\in [S]\backslash\{s\}$ $x\in [S]\backslash\{s\}$](https://dxdy-03.korotkov.co.uk/f/a/2/c/a2c64bab839a702bb1367ba54dd8128d82.png) , , ![$y\in [x^+]\backslash\{s\}$ $y\in [x^+]\backslash\{s\}$](https://dxdy-03.korotkov.co.uk/f/6/3/8/638e1fb4edb1d7d52eab0cbfe20cba9a82.png) . Тогда . Тогда ![$y^+\in [x^+]$ $y^+\in [x^+]$](https://dxdy-03.korotkov.co.uk/f/2/b/e/2be7e6a3960d2cc9ec84a33e3a638c1b82.png) . .Поскольку ![$y\in [x^+]\backslash\{s\}\subseteq S\backslash\{s\}$ $y\in [x^+]\backslash\{s\}\subseteq S\backslash\{s\}$](https://dxdy-01.korotkov.co.uk/f/0/f/a/0fa6ab2094addb679bd324c3b8e700cf82.png) , мы имеем , мы имеем  . .
Покажем, что ![$y^+\in [x^+]$ $y^+\in [x^+]$](https://dxdy-03.korotkov.co.uk/f/2/b/e/2be7e6a3960d2cc9ec84a33e3a638c1b82.png) , т.е. , т.е.  . .
Поскольку ![$x\in [S]$ $x\in [S]$](https://dxdy-04.korotkov.co.uk/f/3/f/2/3f2efd676ada5c2f02f23a683dca1b1d82.png) и и  , мы имеем , мы имеем  . .
Если  , то, очевидно, , то, очевидно,  . .
Пусть теперь  . .
Поскольку ![$y\in [x^+]$ $y\in [x^+]$](https://dxdy-04.korotkov.co.uk/f/7/a/6/7a620fa80f617d175807962d19b6b00482.png) , мы имеем , мы имеем  . .
Если  , то, очевидно, , то, очевидно,  . .
Если же  , то , то  по лемме 1. по лемме 1. Лемма 4. Справедливо включение ![$[S]\in\mathbb S$ $[S]\in\mathbb S$](https://dxdy-02.korotkov.co.uk/f/1/8/0/180de746b380ee3ce2c3371a0c42d5d182.png) . .По определению ![$[S]=\bigl\{y\in S : (\forall\,x\in S)(x\,{\raise.75pt\hbox{$\subset$}\mskip-10mu\lower.75pt\hbox{$\supset$}}\,y)\bigr\}=\{y\in S : [y]=S\}$ $[S]=\bigl\{y\in S : (\forall\,x\in S)(x\,{\raise.75pt\hbox{$\subset$}\mskip-10mu\lower.75pt\hbox{$\supset$}}\,y)\bigr\}=\{y\in S : [y]=S\}$](https://dxdy-04.korotkov.co.uk/f/7/6/c/76c18bb40299b814a15f8e0b64c3efeb82.png) . .
Ясно, что ![$\varnothing\in [S]$ $\varnothing\in [S]$](https://dxdy-03.korotkov.co.uk/f/2/1/c/21cb94c6b14a37defb49986788b1bc6d82.png) . .
Условие ![$(\forall\,Y\subseteq [S])({\cup}Y\in [S])$ $(\forall\,Y\subseteq [S])({\cup}Y\in [S])$](https://dxdy-03.korotkov.co.uk/f/2/9/a/29a1e3f83dd4b401d7b0373c15dffc8282.png) следует из леммы 2 (для следует из леммы 2 (для  ). ).
Осталось показать, что ![$(\forall\,x\in [S]\backslash\{s\})(x^+\in [S])$ $(\forall\,x\in [S]\backslash\{s\})(x^+\in [S])$](https://dxdy-03.korotkov.co.uk/f/e/1/f/e1f5a277b6831c1454b12a72bec2bdd182.png) . .
Итак, пусть ![$x\in [S]\backslash\{s\}$ $x\in [S]\backslash\{s\}$](https://dxdy-03.korotkov.co.uk/f/a/2/c/a2c64bab839a702bb1367ba54dd8128d82.png) . Покажем, что . Покажем, что ![$x^+\in [S]$ $x^+\in [S]$](https://dxdy-02.korotkov.co.uk/f/9/2/d/92dabdb02b6da01d84557fda9c08ee5d82.png) . .
Поскольку ![$x\in [S]\backslash\{s\}\subseteq S\backslash\{s\}$ $x\in [S]\backslash\{s\}\subseteq S\backslash\{s\}$](https://dxdy-03.korotkov.co.uk/f/a/1/b/a1b9a465eec79b909d6970074127085282.png) , мы имеем , мы имеем  . .
Покажем, что ![$[x^+]\in\mathbb S$ $[x^+]\in\mathbb S$](https://dxdy-04.korotkov.co.uk/f/b/f/a/bfa7791598accf47834ac9591654a5b882.png) . .
Ясно, что ![$\varnothing\in [x^+]$ $\varnothing\in [x^+]$](https://dxdy-03.korotkov.co.uk/f/6/2/8/6280b9286b572d6770c00261d397c8e882.png) . .
Условие ![$(\forall\,Y\subseteq [x^+])({\cup}Y\in [x^+])$ $(\forall\,Y\subseteq [x^+])({\cup}Y\in [x^+])$](https://dxdy-01.korotkov.co.uk/f/0/3/5/0359df42489dd03f9fa7bd7796db99dc82.png) следует из леммы 2 (для следует из леммы 2 (для  ). ).
Условие ![$(\forall\,y\in [x^+]\backslash\{s\})(y^+\in [x^+])$ $(\forall\,y\in [x^+]\backslash\{s\})(y^+\in [x^+])$](https://dxdy-01.korotkov.co.uk/f/c/4/4/c44fcc1e10891f5022553b9d6e209b2f82.png) следует из леммы 3. следует из леммы 3. Поскольку ![$[x^+]\in\mathbb S$ $[x^+]\in\mathbb S$](https://dxdy-04.korotkov.co.uk/f/b/f/a/bfa7791598accf47834ac9591654a5b882.png) и и ![$[x^+]\subseteq S=\min\mathbb S$ $[x^+]\subseteq S=\min\mathbb S$](https://dxdy-03.korotkov.co.uk/f/a/4/9/a498ade12e0164f4fea189c57841102d82.png) , мы имеем , мы имеем ![$[x^+]=S$ $[x^+]=S$](https://dxdy-01.korotkov.co.uk/f/4/5/d/45d328d675e8225044046bcea1ebad3482.png) , т.е. , т.е. ![$x^+\in [S]$ $x^+\in [S]$](https://dxdy-02.korotkov.co.uk/f/9/2/d/92dabdb02b6da01d84557fda9c08ee5d82.png) . . Лемма 5. Множество  вполне упорядочено отношением вполне упорядочено отношением  . .Покажем линейность порядка:  или или  . .
По лемме 4 мы имеем ![$[S]\in\mathbb S$ $[S]\in\mathbb S$](https://dxdy-02.korotkov.co.uk/f/1/8/0/180de746b380ee3ce2c3371a0c42d5d182.png) . С другой стороны, . С другой стороны, ![$[S]\subseteq S=\min\mathbb S$ $[S]\subseteq S=\min\mathbb S$](https://dxdy-01.korotkov.co.uk/f/c/f/8/cf8a58837ad68f5e9a08b3dadd0e537a82.png) . .
Следовательно, ![$[S]=S$ $[S]=S$](https://dxdy-04.korotkov.co.uk/f/3/9/6/3960fc520f8afeb6a9dfa554d2d5c7f382.png) , т.е. , т.е.  . . Покажем, что всякое непустое подмножество  имеет наименьший элемент. имеет наименьший элемент.
Итак, пусть  . Покажем, что . Покажем, что  имеет наименьший элемент. имеет наименьший элемент.
Положим  . .
Достаточно показать, что  имеет наименьший элемент. имеет наименьший элемент.
Положим  . .
Как легко видеть,  . .
Положим  . .
Поскольку  , мы имеем , мы имеем  . .
Поскольку  , мы имеем , мы имеем  , т.е. , т.е.  . .
Если  , то с учетом , то с учетом  мы имеем мы имеем  . .
Пусть теперь  , т.е. , т.е.  . .
Заметим, что  и и  . .
Поскольку  и и  , мы имеем , мы имеем  . .
Поскольку  , мы имеем , мы имеем  . .
Поскольку  , мы имеем , мы имеем  , т.е. , т.е.  . .
Покажем, что  . .
Если бы нашелся  такой, что такой, что  , то мы бы , то мы бы
имели  , что, очевидно, невозможно. , что, очевидно, невозможно. Лемма 6. Функция  является биекцией является биекцией  на на  . .Пусть  , ,  . Покажем, что . Покажем, что  . .
Не нарушая общности, будем считать, что  . .
Поскольку  , мы имеем , мы имеем  . .
Ясно, что  . .
Следовательно,  , а значит, , а значит,  . .
С другой стороны,  и поэтому и поэтому  . . Пусть  . Покажем, что . Покажем, что  . .
Положим  и и  . .
Поскольку  , мы имеем , мы имеем  , т.е. , т.е.  . .
По определению  мы имеем мы имеем  . В частности, . В частности,  . .
Поскольку  , мы имеем , мы имеем  . .
Покажем, что  . .
Действительно, если бы  , то с учетом , то с учетом 
мы бы имели  и тем самым и тем самым  , ,
что противоречит соотношениям  и и  . . Из лемм 5 и 6 следует, что множество  может быть вполне упорядочено.
|
|



