Текст анонсированного доказательства можно скачать в виде
PDF-файла.
По традиции этот текст дублирован ниже в теле сообщения.
(Опять-таки, ничего нового. Просто доказательство известного факта.
Основная возня связана с обоснованием рекурсивного построения
функции по элементам вполне упорядоченного множества.)
Итак...
Любое вполне упорядоченное множествопорядково изоморфно некоторому ординалуПодробное доказательство в ZFCДля упорядоченного множества

и элемента
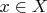
условимся
обозначать множество

символом

.
Индукция по элементам вполне упорядоченного множестваДля любой теоретико-множественной формулы 
следующее утверждение является теоремой ZFC.
Если  — произвольное вполне упорядоченное множество
— произвольное вполне упорядоченное множество
и для любого  из
из  следует
следует  ,
,
то  для всех
для всех  .
.
Положим  .
.
Предположим вопреки доказываемому, что  .
.
Положим  .
.
Поскольку  , мы имеем
, мы имеем  .
.
Следовательно,  , что противоречит включению
, что противоречит включению  .
.
Обозначим через

формализацию утверждения
« множество  является функцией с областью определения
является функцией с областью определения  ».
».
Для

и

положим
![$f[E]:=\{f(e):e\in E\}$ $f[E]:=\{f(e):e\in E\}$](https://dxdy-02.korotkov.co.uk/f/5/d/b/5dbf635152c0dd9e46a6f5445c2390bb82.png)
.
Всюду ниже

— произвольное вполне упорядоченное множество.
Для
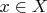
и

будем писать

вместо
![$(\forall\,y\in x{\downarrow})\bigl(\,f(y)=f[y{\downarrow}]\,\bigr)$ $(\forall\,y\in x{\downarrow})\bigl(\,f(y)=f[y{\downarrow}]\,\bigr)$](https://dxdy-02.korotkov.co.uk/f/d/a/f/daf02b02da84b775de2ebb93769829a082.png)
.
Положим

.
Лемма 1.
Если  , то
, то  .
.Пусть 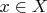 ,
,  ,
,  и
и  .
.
Докажем  индукцией по
индукцией по  .
.
Пусть  и
и  . Покажем, что
. Покажем, что  .
.
Из  следует
следует ![$f(y)=f[y{\downarrow}]$ $f(y)=f[y{\downarrow}]$](https://dxdy-03.korotkov.co.uk/f/6/0/f/60f346818a1c2cace3ea38964a84c72682.png) .
.
Из  следует
следует ![$g(y)=g[y{\downarrow}]$ $g(y)=g[y{\downarrow}]$](https://dxdy-03.korotkov.co.uk/f/a/7/0/a700687e14049f98e8380bb2f1b26d2682.png) .
.
Из  следует
следует ![$f[y{\downarrow}]=g[y{\downarrow}]$ $f[y{\downarrow}]=g[y{\downarrow}]$](https://dxdy-01.korotkov.co.uk/f/4/5/7/457b84e68b3720e8b9615164d78cd63f82.png) .
.
Таким образом, для всякого

имеется единственная функция

,
удовлетворяющая условию

, т.е. такая, что
![$f^x(y)=f^x[y{\downarrow}]$ $f^x(y)=f^x[y{\downarrow}]$](https://dxdy-02.korotkov.co.uk/f/9/e/d/9ed5acb87ea896d9623a355df5f874f482.png)
для всех

.
Лемма 2.
Пусть  и
и  . Тогда
. Тогда  и
и  .
.Как легко видеть, из  вытекает
вытекает  .
.
Следовательно,  .
.
Поскольку  и
и  , мы имеем
, мы имеем  по лемме 1.
по лемме 1.
Определим функцию

, полагая
(Отметим, что существование такой функции

можно обосновать
с помощью схемы аксиом подстановки.)
Лемма 3.
Пусть  . Тогда
. Тогда ![$F(x)=F[x{\downarrow}]$ $F(x)=F[x{\downarrow}]$](https://dxdy-04.korotkov.co.uk/f/f/0/b/f0b01813311322e06c8c9ecaa645a8aa82.png) .
.Покажем, что  .
.
Пусть  . Покажем, что
. Покажем, что  .
.
По лемме 2 мы имеем  и
и  .
.
Следовательно, ![$F(y)=f^y[y{\downarrow}]=f^x|_{y{\downarrow}}[y{\downarrow}]=f^x[y{\downarrow}]=f^x(y)$ $F(y)=f^y[y{\downarrow}]=f^x|_{y{\downarrow}}[y{\downarrow}]=f^x[y{\downarrow}]=f^x(y)$](https://dxdy-02.korotkov.co.uk/f/9/e/4/9e4ffe348538d6753755de16465e14b582.png) .
.
Таким образом, ![$F(x)=f^x[x{\downarrow}]=F|_{x{\downarrow}}[x{\downarrow}]=F[x{\downarrow}]$ $F(x)=f^x[x{\downarrow}]=F|_{x{\downarrow}}[x{\downarrow}]=F[x{\downarrow}]$](https://dxdy-02.korotkov.co.uk/f/1/7/c/17c797cc8c4d0a35de1fb54d902e42f282.png) .
.
Лемма 4.
Справедливо равенство  .
.Достаточно показать, что  .
.
Докажем последнее утверждение индукцией по 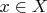 .
.
Пусть 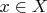 и
и  . Покажем, что
. Покажем, что  .
.
Пусть  . Покажем, что
. Покажем, что ![$F|_{x{\downarrow}}(y)=F|_{x{\downarrow}}[y{\downarrow}]$ $F|_{x{\downarrow}}(y)=F|_{x{\downarrow}}[y{\downarrow}]$](https://dxdy-03.korotkov.co.uk/f/6/5/2/652e8a12e80e128a8be6d0d9099d203a82.png) .
.
Поскольку  , мы имеем
, мы имеем  .
.
По лемме 3 мы имеем ![$F(y)=F[y{\downarrow}]$ $F(y)=F[y{\downarrow}]$](https://dxdy-03.korotkov.co.uk/f/a/5/f/a5f7abc6efd02d21eaa4d5466a2c397182.png) .
.
Следовательно, ![$F|_{x{\downarrow}}(y)=F(y)=F[y{\downarrow}]=F|_{x{\downarrow}}[y{\downarrow}]$ $F|_{x{\downarrow}}(y)=F(y)=F[y{\downarrow}]=F|_{x{\downarrow}}[y{\downarrow}]$](https://dxdy-03.korotkov.co.uk/f/6/8/2/6824f2dec9caa6b38681482d87814bd182.png) .
.
Лемма 5.
Для всякого 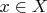 мы имеем
мы имеем  .
.
В частности, если  и
и  , то
, то  .
.Утверждение леммы 5 непосредственно вытекает из лемм 3 и 4.
Лемма 6.
Для всякого 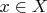 множество
множество 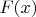 является ординалом.
является ординалом.Покажем, что для всякого 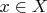 множество
множество 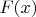 транзитивно.
транзитивно.
Пусть 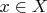 и
и  . Покажем, что
. Покажем, что  .
.
По лемме 5 найдутся  такие, что
такие, что  ,
,  и
и  .
.
Поскольку  , по лемме 5 мы имеем
, по лемме 5 мы имеем  .
.
Покажем, что для всякого 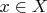 все элементы множества
все элементы множества 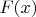 транзитивны.
транзитивны.
По лемме 5 все элементы множества 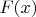 имеют вид
имеют вид  ,
,
а значит, они транзитивны по доказанному выше.
Таким образом, для всякого 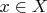 множество
множество 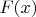 транзитивно
транзитивно
и все его элементы транзитивны, т.е. 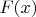 является ординалом.
является ординалом.
Положим
![$A:=F[X]=\{F(x):x\in X\}$ $A:=F[X]=\{F(x):x\in X\}$](https://dxdy-03.korotkov.co.uk/f/6/6/f/66fb6ddc461e15d4dfe919b35e8f07b882.png)
.
Лемма 7.
Множество  является ординалом.
является ординалом.По лемме 6 все элементы множества  транзитивны.
транзитивны.
Остается показать, что само множество  транзитивно.
транзитивно.
Пусть  . Покажем, что
. Покажем, что  .
.
Поскольку  , имеется
, имеется 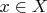 такой, что
такой, что  .
.
Поскольку  , по лемме 5 имеется
, по лемме 5 имеется  такой, что
такой, что  .
.
Следовательно,  .
.
Лемма 8.
Функция  является порядковым изоморфизмом
является порядковым изоморфизмом  на ординал
на ординал  .
.По определению  функция
функция  является сюръекцией
является сюръекцией  на
на  .
.
Покажем, что для любых  из
из  следует
следует  .
.
По лемме 5 из  следует
следует  , т.е.
, т.е.  .
.
Покажем, что для любых  из
из  следует
следует  .
.
Пусть  . Покажем, что
. Покажем, что  .
.
Если бы 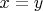 или
или  , то с учетом доказанного выше мы бы имели
, то с учетом доказанного выше мы бы имели
 или
или  вопреки неравенству
вопреки неравенству  .
.
Следовательно,  (в силу линейности порядка на
(в силу линейности порядка на  ).
).