
Для всех четных значений показателя степени

сумма

где

и

- натуральные нечетные, не равна

где

натуральное четное. Положим

где

- четные числа. Запишем сумму

в виде


Нетрудно видеть, что для любых четных чисел

и

, в левой части этого неравенства всегда четное число, у которого все слагаемые, кроме последнего равного 2, делятся на 4, а в правой части четное число, которое также делится на 4. После деления обеих частей на 2 получим, что слева от знака неравенства нечетное число, а справа число четное. Следовательно, неравенство справедливо, а равенство возможно тогда, когда четное число

делится только один раз на 2. В этом случае число

является иррациональным числом.

Для четного

сумма

где

- натуральное четное,

- натуральное нечетное, не равна

где

натуральное нечетное. Положим, что

где

- натуральное нечетное число. Тогда сумма

запишется в виде

Обозначим

Тогда

Для четных

целочисленный многочлен 4-ой степени

есть число четное, а сумма

есть число нечетное. Для нечетных

целочисленный многочлен 4-ой степени

неприводим над кольцом целых чисел и над полем рациональных чисел согласно критерия Эйзенштейна (коэффициент при старшем члене не делится на простое число

, коэффициенты всех остальных членов делятся на

, а свободный член равный

не делится на

)[1]. Неприводимость многочлена над кольцом целых чисел и над полем рациональных чисел означает, что его невозможно разложить на множители - целочисленные многочлены степеней меньших чем

. Следовательно, строго положительное число

, представленное в виде неприводимого многочлена, не может быть целой степенью натурального числа.

Можно показать, что для всех нечетных значений показателя степени

строго положительная разность

где

,

- натуральные нечетные, не равна

где

- натуральное четное. Обозначим разность

– четное число, так как

и

- нечетные. Запишем разность

в виде

Обозначим

Тогда соотношение (i) перепишется так:

Рассмотрим целочисленный многочлен в круглых скобках в (ii) для простых значений показателя степени


Согласно критерия Эйзенштейна многочлен

неприводим над кольцом целых чисел и над полем рациональных чисел в силу того, что коэффициент при старшем члене не делится на простое число
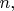
коэффициенты всех остальных членов делятся на

, а свободный член равный

не делится на

)[1]. Неприводимость многочлена

над кольцом целых чисел и над полем рациональных чисел означает, что его невозможно разложить на множители - целочисленные многочлены степеней меньших чем

. Следовательно, строго положительное число

, представленное в виде неприводимого многочлена, не может быть целой степенью натурального числа.
Получаем

и в силу неприводимости

разность

.

Для всех нечетных значений показателя степени

сумма

, где

- натуральные нечетные, не равна

, где

- натуральное четное. Предполагая, без ограничения общности рассуждений, что

, запишем

и

в виде:

, где

Тогда

Раскрывая биномы, получим
![$x^{n} + y^{n} = (S + q)^{n} + (S - q)^{n} = 2Sq^{n - 1}(S^{n - 1}/q^{n - 1} + [n(n - 1)/2]S^{n - 3}/q^{n - 3} + [n(n - 1)(n - 2)(n - 3)/24]S^{n - 5}/q^{n - 5} + \ldots + [n(n - 1)(n-2)/6]S^2/q^2 + n)~~ (iii) $ $x^{n} + y^{n} = (S + q)^{n} + (S - q)^{n} = 2Sq^{n - 1}(S^{n - 1}/q^{n - 1} + [n(n - 1)/2]S^{n - 3}/q^{n - 3} + [n(n - 1)(n - 2)(n - 3)/24]S^{n - 5}/q^{n - 5} + \ldots + [n(n - 1)(n-2)/6]S^2/q^2 + n)~~ (iii) $](https://dxdy-02.korotkov.co.uk/f/9/1/5/9159c10d290438b6eae9da97e4fa792a82.png)
Обозначим

Тогда соотношение (iii) перепишется так:
![$$x^{n} + y^{n} = (S + q)^{n} + (S - q)^{n} = 2Sq^{n - 1}(w^{n - 1} + [n(n - 1)/2]w^{n - 3} + [n(n - 1)(n-2)(n-3)/24]w^{n - 5} + \ldots + [n(n - 1)(n-2)/6]w^2 + n) $$ $$x^{n} + y^{n} = (S + q)^{n} + (S - q)^{n} = 2Sq^{n - 1}(w^{n - 1} + [n(n - 1)/2]w^{n - 3} + [n(n - 1)(n-2)(n-3)/24]w^{n - 5} + \ldots + [n(n - 1)(n-2)/6]w^2 + n) $$](https://dxdy-03.korotkov.co.uk/f/2/d/5/2d5fbb813fa6ffd12f32d83f3a7fbd5082.png)
Рассмотрим целочисленный многочлен в круглых скобках в (iii) для простых значений показателя степени

![$$ F(w) = w^{n - 1} + [n(n - 1)/2]w^{n - 3} + [n(n - 1)(n-2)(n-3)/24]w^{n - 5} + \ldots + [n(n - 1)(n - 2)/6]w^2 + n $$ $$ F(w) = w^{n - 1} + [n(n - 1)/2]w^{n - 3} + [n(n - 1)(n-2)(n-3)/24]w^{n - 5} + \ldots + [n(n - 1)(n - 2)/6]w^2 + n $$](https://dxdy-01.korotkov.co.uk/f/4/5/c/45c0e3aea7cf60704df9ae855af61add82.png)
Согласно критерия Эйзенштейна многочлен

неприводим над кольцом целых чисел и над полем рациональных чисел в силу того, что коэффициент при старшем члене не делится на простое число

, коэффициенты всех остальных членов делятся на

, а свободный член равный

не делится на

)[1]. Неприводимость многочлена

над кольцом целых чисел и над полем рациональных чисел означает, что его невозможно разложить на множители - целочисленные многочлены степеней меньших чем

. Следовательно, строго положительное число

, представленное в виде неприводимого многочлена, не может быть целой степенью натурального числа. Получаем

и в силу неприводимости

сумма

.
I. Рассмотрим однородное диофантово уравнение вида

при этом

- целые ,

Постановка задачи - принадлежат ли решения этого уравнения кольцу целых чисел

при различных значениях показателя

[2],[3],[4],[5],[6].
Нетрудно видеть, что уравнение (1) при

имеет целочисленные решения. Например, при
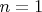
значения

и

а при
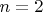
значения

и

удовлетворяют уравнению (1).
Далее утверждается, что уравнение (1) при

не имеет натуральных решений

. Доказательство этой старой задачи строится от противного, т.е. предполагается, что равенство в (1) возможно. Приведённые выше четыре соотношения показывают, что в уравнении (1), в котором

- целые,

, для всех четных и нечетных показателей степени

равенство невозможно. Так для

соотношения 1 и 2 показывают, что уравнение (1) не имеет натуральных решений

, а для простых нечетных

соотношение 3 показывает, что уравнение (1) не имеет натуральных решений

, если

- четное число,

и

- нечетные числа (равносильная запись (1)

), а если

и

- нечетные числа, а

- четное, то соотношение 4 показывает, что сумма

.
Очевидно, что если неразрешимость уравнения (1) в целых числах доказана для некоторого показателя

, то тем самым это доказано и для всех показателей, кратных

, так как всякое целое

делится или на 4, или на нечетное простое число, то можно ограничиться случаями, когда показатель

равен либо 4, либо нечетному простому числу [2], [4], [5], [6].

II. Далее, если рассматривать (1) для всех целых

, то равенство в (1) возможно только для

Легко видеть, при

(получается 2 = 1) равенство не выполняется.
Рассмотрим (1) с показателем степени


- не равные нулю целые числа.
Нетрудно видеть, что для

равенство имеет место, например, при четных равных друг другу

и

- целое.
При

и, к примеру, при

и

равенство (1) выполняется.
Пусть

тогда (1) запишется так:

где

Ясно, что в (2)

и


Пусть

целое, тогда правая часть (3) есть

- ая степень целого числа. Из доказанного выше в разделе I следует, что (3) не имеет целочисленных решений для всех значений показателя степени

и , следовательно, равенство (1) не выполняется для всех

если

- не равные нулю, целые числа.
III. Пусть в (1) для всех целых

, числа

- рациональные, т.е.

где

– целые, не равные нулю, числа.
IV. Пусть в (1) для всех целых

числа

- иррациональные.
V. Пусть в (1) для всех целых

числа

- комплексные, т.е.

где

, а числа

- вещественные.
Для задач III, IV, V определить условия равенства.
Список литературы
1. Курош А. Г. Курс высшей алгебры. М.: Наука, изд. 9-е, 1968.
2. Эдвардс Г. М. Последняя теорема Ферма. Генетическое введение в алгебраическую теорию чисел. -М.: МИР, 1980.
3. Куликов Л. Я. Алгебра и теория чисел. -М.: Высшая школа, 1979.
4. Блинов В. Ф. Великая теорема Ферма: Исследование проблемы -М.: Изд-во ЛКИ,2008.
5. Постников М. М. Теорема Ферма. Введение в теорию алгебраических чисел. -М.: Наука, 1978.
6. Рибенбойм П. Последняя теорема Ферма для любителей. –М : Мир, 2003.



