Здравствуйте! Подскажите, пожалуйста, основной принцип работы моста в следующей задаче.
Цепной мост длиной АВ = 20 м поддерживается двумя цепями; стрела провисания цепей СК=2 м; нагрузка моста составляет 1,6 т на погонный метр. Определить натяжение цепи в средней точке С, зная, что кривая, на которой лежат вершины веревочного многоугольника ADECFGB, — парабола.

1) Я так поняла, что верёвочный многоугольник показан на рисунке. По нему нужно построить силовой многоугольник, откуда и взять значение силы
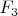
, так как она будет по модулю равна равнодействующей сил натяжений

и

.
2) С другой стороны, если мост - твёрдое тело, то указанная нагрузка в условии должна распределяться и на опоры моста.
3) Если цепной мост держится на двух цепях, то нагрузка должна учитываться поровну на каждую цепь?



