Задача
ММ113 утратила статус конкурсной и может свободно обсуждаться на форуме.
===============Результат Задачи ММ113 учитывается дважды: в тематическом конкурсе и в основном Марафоне.
ММ113 (Ш-3) (10 баллов)
На множестве полей шахматной доски определим структуру графа

следующим образом:
две вершины (два поля) будем считать смежными, если конь может за один ход переместиться из одной вершины в другую.
Аналогично определим граф слона

, граф ладьи

, граф ферзя

и граф короля

.
Для каждого из этих графов:
1. Найти
а) количество ребер;
б) количество компонент связности;
в) радиус и диаметр каждой компоненты;
г) наибольшую клику.
2. Выяснить является ли граф:
а) двудольным;
б) эйлеровым;
в) гамильтоновым;
г) планарным?
================РешениеОтветы на большинство пунктов задачи находятся легко. Поэтому приведу лишь краткие пояснения к решению и ответ в виде таблицы.
1.а. Количество ребер большинства графов легче всего найти как полусумму степеней всех вершин. Разумеется, при этом следует использовать симметричность доски.
Например, для графа коня искомое число ребер равно

.
Для графа ферзя проще просто просуммировать количества ребер в графах ладьи и слона.
1.б. У графа слона две компоненты связности (черные и белые поля). Остальные графы, очевидно, связны.
1.в. Диаметр и радиус графов ладьи и ферзя, а также каждой компоненты связности графа слона, очевидно, равны 2.
Тривиально проверяется, что из каждого из полей d4, d5, e4, e5 король может добраться до любого поля не более чем за 4 хода. Поэтому радиус графа короля - 4.
В то же время, на маршрут от любого края до противоположного края доски королю понадобится 7 ходов. Поэтому диаметр графа короля - 7.
Наиболее содержательная задача - нахождение диаметра и радиуса графа коня. Ее можно решить, найдя поиском в ширину эксцентриситеты всех вершин графа коня.
Поиск в ширину можно провести в табличке 8х8 клеток вручную: помещаем 0 в начальную клетку; ставим 1 во все клетки, смежные начальной; ставим 2 во все свободные клетки, смежные клеткам. помеченным 1; и т.д.
В последней заполненной клетке будет записан эксцентриситет начальной вершины.
Разумеется, нет никакой необходимости применять данный алгоритм ко всем 64-м вершинам графа коня. По соображениям симметрии достаточно обследовать поля a1, b1, b2, c1, c2, c3, d1, d2, d3, d4.
1.г. Наибольшие клики в графах слона (большая диагональ) ладьи (любая горизонталь или вертикаль) и ферзя содержат по 8 вершин.
Наибольшая клика в графе короля (любой квадрат 2х2) содержит 4 вершины.
Поскольку среди любых трех полей найдутся, по крайней мере, два одноцветных, в графе коня не может быть клики, содержащей более двух вершин.
2.а. Граф коня (в котором смежными могут быть только разноцветные поля) двудолен.
Наличие клик, содержащих более двух вершин, гарантирует отсутствие двудольности в остальных графах.
2.б. Граф ладьи, степень каждой вершины которого равна 14, эйлеров. В остальных графах есть вершины нечетных степеней.
2.в. Граф слона не связен и потому не гамильтонов. Гамильтонов цикл в графе коня и в остальных графах (один для всех) приведены на рисунках, заимствованных у Николая Дерюгина.

 2.г.
2.г. Ни один из графов не планарен. В графах слона, ладьи и ферзя есть пятивершинные клики, а в графах короля и коня легко отыскать подграфы, стягиваемые, например, к
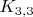
.
Ответ:
 Обсуждение
ОбсуждениеБольшинство пунктов задачи тривиальны. цена в 10 баллов отражает не сложность, а количество задачек, объединенных под общей шапкой ММ113. Правильность такого подхода косвенно подтвердили и сами участники, большинство из которых не обошлось без ошибок. Значительная часть этих ошибок была устранена марафонцами еще до публикации разбора задачи, а остальные нашли отражение в призовых баллах за задачу.
Наиболее содержательный пункт задачи (о гамильтоновости графа коня) является, к сожалению, и наиболее известным. Поэтому я вполне согласен (что бывает со мной редко

) с теми участниками, которые не слишком высоко оценили эстетическую сторону задачи, (хотя и с теми, кому задачка понравилась, тоже спорить не буду

).
НаградыЗа решение задачи ММ113 Алексей Волошин получает 11 призовых баллов (1 балл добавлен за доскональное обоснование каждого пункта), Сергей Половинкин, Анатолий Казмерчук и Виктор Филимоненков получают по 10 призовых баллов, Николай Дерюгин и Кирилл Веденский получают по 9 призовых балла, а Эдвард Туркевич - 8 призовых баллов.
Эстетическая оценка задачи - 3.8 балла-- 23 окт 2009, 19:11 --================Текущее положение участников
в XII туре Математического марафона