Задача статистики

[taranov_a]

Здравствуйте, прошу Вашей помощи в решении задачи.
Я исчерпал (как мне кажется все методы), последняя надежда на Вас ув. Математики.
Задача:
Автодром, на автодроме 6 машин. Моя задача по сумме токов определить кол-во катающихся машин.
Средний ток одной машины 44 условных единицы. Т.е. если средний ток за период = 88 /44(средний ток одной машины)= 2 машины ездило.
Но ток одной машины может колебаться от [20.. 120] условных единицы, в зависимости от агрессивности езды.
То средний ток за период для двух машин при агрессивной езде стремиться к 240. и если я его разделю на средний ток одной машины я получу не верный результат.
Пожалуйста, наведите на правильную мысль.
График езды 3 – человек

График езды 2 – человек

[vsufiy]

На мой взгляд, здесь типичная задача дискриминантного анализа (распознования образов). Методов решения достаточно много: традиционный дискриминатный анализ (предложеный Фишером), логистический регрессионный анализ, нейронные сети, деревья решений и т.д. Важные результаты получены академиком Ю.И. Журавлевым и его учениками.
Основная проблема которую нужно решить выбор структуры исходных данных. Необходимо провести исследования езды от 1 до 6 человек.
На вскидку, можно посоветовать исследовать скользящие средние. Кстати, если не секрет, зачем нужно решать эту задачу, не легче ли просто посмотреть на автодром?

[Dan_Te]

А машина может постоянно ездить на мощности 120?
Судя по вашим графикам, не может.

[taranov_a]

Спасибо Вам что откликнулись.
Ув. Vsufiy касательно «зачем так делать, если можно посмотреть»: я, инженер, мне руководство поставило задачу создать датчик отображающий суммарное количество клиентов автодрома за сутки, вот я и парюсь.
Насчёт подхода: мне хотелось бы проработать не сколько алгоритмов.
И я их стараюсь разделить по сложности реализации, по предварительным расчётам дискриминантный анализ у устройства вычисления ( 8-ми разрядный микроконтроллер) недостаток вычислительных средств. Но в любом случае если ничего не поможет я буду стараться его реализовать.
Скользящее усреднение не помогло, погрешность не допустимо высока, >=20 %.
Ув. Dan_Te если машина упрется в перпятствие и педаль будет нажата то до ток -> 120 у.е. Но это можно рассматривать как частный случай. Где частность события ~ 0.05.

На данном этапе хотелось бы реализовать корреляционный фильтр, но о нем я только слышал к сожалению в Интернете я ничего не нашёл, и соответствующей литературы под боком нет.

[Dan_Te]

А что такое "скользящее среднее"? Это рассматривать функцию
$F(x)=\frac 1 x \int\limits_0^x f(t)dt$,
где $f(t)$ - функция, графики которой изображены выше?

[vsufiy]

Супермодератор:

Цитата:

А что такое "скользящее среднее"?

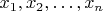
Пусть $x_1, x_2, \ldots, x_n$ - последовательность чисел, представленных на графиках. Естественно считать, что на графиках представлены не сами функции, а именно значения функций, которые измеряются в дискретные такты времени.
Скользящее среднее - это значения:

$$\bar x_k = \sum_{i=-t_l}^{t_h}{\alpha_i x_{i+k}},\ \ \ k=t+1, t+2, \ldots, n-t $$

,
где $\alpha_i$ - весовые коеффициенты, такие, что

$$\sum_{i=-t_l}^{t_h}{\alpha_i}=1$$

;
$t_l$ и $t_h$ - параметры, которые можно варьировать.
В указанном случае можно принять, например, $t_h = 0$, а весовые коэффициенты одинаковые

$$\alpha_i = \frac{1}{t_l+1}$$

.

taranov_a:

Цитата:

И я их стараюсь разделить по сложности реализации, по предварительным расчётам дискриминантный анализ у устройства вычисления ( 8-ми разрядный микроконтроллер) недостаток вычислительных средств.

Дискриминантый анализ используется "off-line", т.е. вы записали данные на какой-нибудь носитель, для поездок только 1, только 2, ... или только 6-х машин. Далее можно сравнить:
1) законы распределения выборок для каждого из состава машин;
2) скользящие средние (при различных $t_l$ и $\alpha_i$, и выбрать при каких значениях будет лучшее разделение, кстати можно выбрать несколько разных $t_l$ и $\alpha_i$;
3) выборочные дисперсии;
4) и др. характеристики.

Сначала это можно сделать визуально (или с помощью дисперсионного анализа проверить отличаются ли выборочные средние). Сравнить, отличаются ли дисперсии и т.д.
После этого с помощью дискриминантного анализа составляются дискриминантные функции (т.е. коэффициенты), которые можно прошить в микроконтроллер, т.е. в процессе работы "online" дискриминантый анализ не проводится, а используются лишь результаты ДА.
Гипотеза о том, что средние для разл. кол-ва машин будут отличаться не вызывает сомнений.
Гипотезу же о разных дисперсиях выдвинул в связи с тем, что с увеличением количества машин вариабельность графиков должна уменьшаться.
Интервалы, где нулевые значения - можно наверное как-то исключить (или обрабатывать), поскольку они, по моему мнению, будут искажать результаты. Возможно здесь я и ошибаюсь.
P.S. Дисперсии тоже считать "скользящие".
P.P.S. Методов достаточно много, например, в литературе очень часто находил примеры использования нечеткой логики в технических системах. Тем не менее, на мой взгляд здесь первоначальная задача в правильном выборе признакового постранства.

[taranov_a]

Спасибо Вам ув. vsufiy.
Вы совершенно правы :

Цитата:

Гипотезу же о разных дисперсиях выдвинул в связи с тем, что с увеличением количества машин вариабельность графиков должна уменьшаться

и

Цитата:

Интервалы, где нулевые значения - можно наверное как-то исключить (или обрабатывать).

Задача решена с допустимой погрешностью 2% следующим образом.
Заранее прошу прощения , формулировки могут быть не корректными.
1. «Сглаживание» функции тока методом скользящего усреднения (нули исключены) с коэффициентами полученными в ходе практических испытаний.
2. Получения функции «плотности тока»
3. Дисперсионный анализ.
Касательно не чёткой логики, то этот метод мною рассматривался, могу сказать что этот метод не приемлем для решения этой задачи (могу и ошибаться) т.к. провели фазификацию, объявили лингвистические переменные, функции принадлежности……… дефазификация -> алгоритм.
В результате получил что не четкий алгоритм решает задачу чётко.
На данный момент времени я не располагаю знаниями о Дискриминантном анализе, но в ближайшее время его освою и для удовлетворения собственных амбиций применю при решении данной задачи.

Спасибо что на толкнули на интересные мысли и на новые концепции. Тема закрыта. Творческих успехов.
[/quote]