Вот мои рассуждения:
1. Для того чтобы оценить максимальную высоту на которую
можно подняться, мы будем полагать, что забег делает человек
с почти идеальными характеристиками, это значит, что его физические
характеристики не хуже чем у лучших спортсменов. В среднем человек может
приземлится на ноги спрыгнув с

метровой высоты. При подлете к земле,
его скрость будет равна

м/c. Отсюда можно сделать вывод,
что при забеге на стенку, скорость должна быть меньше этой! Пусть человек подбегает к стенке
со скоростью

. Сталкиваясь со стенкой, он начинает, забираться на нее, перебирая ногами.
Обозначим время столкновения со стенкой

, тогда будем считать, что

,
где

- средняя сила действующая, со стороны стенки на человека.
Значит, что после забирания на стенку , человек отпрыгивает, от нее с такой же скоростью.
Сила трения

и будет поднимать человека вверх.
Врямя

будет определяться временем, опрокидывания спортсмена, на спину, оценим его:
Спортсмена, будем моделировать стержнем, длины

м. Перейдем в НИСО, связанную со
спортсменом, видно что момент сил, относительно точки касания спортсменом стены, это есть

.
В итоге получаем:

.
Откуда

.
Следовательно:

.
Таким образом:

, где

и

- начальный и конечный угол
между бегуном и стенкой.Пусть интеграл в данных пределах равен
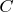
. И так:

. Но так как

,
то:

.
Человек поднимет свой центр масс на высоту:

Таким образом:

.
Найдем максимум этой функции в зависимости от
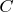
.
Взяв, производную по

и приравняв ее к нулю, в итоге получим:

,

, следовательно:

.
Конечно при подбеге к стенке человек подпрыгнет, и затем будет карабкаться.
Хорошие спортсмены, брыгают на

м в высоту.
И так если человек бежит на стенку со скоростью

м/c,
то он поднимет свой центр масс на велечину:

м.
Это значит, что стопы ног спортсмена ,коснутся двух метровой высоты, сам же центр масс будет выше.
И так:

м.
Ответ:

м.




