TOTALОбратимость ходов - нетривиальная часть задачи.
Я скоро набросаю доказательство.
-- Mon Jun 01, 2009 02:35:13 --Доказательство.
Позицией назовем вектор

, где

количество карт в

-й кучке и

- номер кучки из которой предстоит сделать ход, причем

,

и

для всех

.
Пусть

- это функция, которая позицию

переводит в новую позицию, раскидывая карты из кучки

согласно правилам.
Докажем, что для каждой позиции

найдется по крайней мере одна позиция

, для которой

. Рассмотрим в

кучки с минимальным количеством карт, а среди них самую левую - пусть ее номер равен

(таким образом, для

мы имеем

, а для

- соответственно

).
Возможны следующие случаи:
1) Если

, то положим

2) если

и существует такое

, что

, то переопределим

равным минимальному такому

, попадая таким образом в случай 1) рассмотренный выше;
3) если

и для всех

выполняется

, то положим

Обозначим это построение через

. Для заданной позиции

вектор

также является позицией. Причем, как нетрудно проверить,

.
Пусть

- произвольная позиция. Рассматривая последовательные итерации

на

, из конечности числа различных позиций, заключаем, что либо

для некоторого натурального

, либо существует такие неотрицательные целые числа

и

, что

и

. Второй вариант, однако, невозможен, так как в нем получается противоречие:

Итак, получаем, что

для некоторого натурального

, а значит и

, то есть начав с произвольной позиции

мы обязаны в нее же и вернуться при итерациях
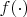
.
Другими словами, мы доказали, что

и

являются взаимно-обратными перестановками на множестве позиций.



