Ниже приводится "школьное" доказательство того факта, что объем

-мерного куба стремится к 0.
Будем обозначать

- объем

-мерного тела. Индексом в данной записи может быть:
sp - шар (sphere);
cl - цилиндр (cylinder);
cn - конус (cone);
tc - усеченный конус (truncated cone).

-мерные тела (все определения приближены к "школьным", точность не гарантируется):
1. Шар - г.м.т., расстояние от которых до некоторой центральной точки (центра шара), не превышает некоторого конечного расстояния (радиуса шара). Объем

-мерного шара:

(1),
где

- некоторая константа (при

она равна 2, при

-

, при

-

и т.д.; реальное точное ее значение нам не понадобится, поэтому в дальнейших выкладках она будет фигурировать без конкретизации),

- радиус шара.
Двухмерный шар - круг.
2. Цилиндр - часть

-мерного пространства, "заметаемая" при перемещении шара

-го порядка вдоль направления, перпендикулярного подпространству, в котором расположен шар, на некоторое конечное расстояние (высоту цилиндра). Объем

-мерного цилиндра:

, где

- радиус основания цилиндра,

- его высота.
Из такого определения следует, что объем цилиндра равен:

(2)
Двухмерный цилиндр - прямоугольник.
3. Конус - отличается от цилиндра тем, что перемещении шар

-го порядка равномерно уменьшается (точнее, уменьшается его радиус), постепенно стягиваясь в точку (вершину конуса). Расстояние, пройденное к этому моменту - высота конуса. Радиус шара уменьшается пропорционально пройденному расстоянию. Объем

-мерного конуса:

, где

- радиус основания конуса,

- его высота.
Основываясь на приведенном выше определении и обладая простейшими навыками интегрирования, можно заключить, что

(3)
Двухмерный конус - равнобедренный треугольник.
4. Усеченный конус - отличается от обычного конуса тем, что шар прекращает свое движение до того, как стянется в точку. Объем

-мерного усеченного конуса:

, где

и

- радиусы оснований усеченного конуса (подразумевается, что

),

- его высота.
Объем усеченного конуса можно найти тем же способом, которым он находится для трехмерного случая (с использованием формулы (3)):

Двухмерный усеченный конус - равнобочная трапеция.
Конечно, все приведенные выше "определения" - чистой воды "математическая алхимия", но школьникам ("продвинутым") могут быть интуитивно понятны.
Будем рассматривать шар диаметра 1 (радиус шара

), так как все остальные случаи сводятся к этому простым масштабированием или заменой единиц измерения длины (как уже было замечено выше).
1. Заметим, что

-мерный шар радиусом

полностью "помещается" в

-мерный цилиндр радиусом

и высотой

. То есть

Откуда

(в нашем случае),
что говорит о том, что объем шара диаметра 1 уменьшается с увеличением размерности шара. Однако у последовательности

может быть предел, не равный нулю. Докажем, что его нет.
2. "Спилим" с торцов описанного цилиндра фаску размером

от радиуса основания цилиндра (под углом 45 градусов, для простоты). После такой операции цилиндр превратится в тело, состоящее из двух одинаковых усеченных конусов (с радиусами основания

и

, высотой

) и центрального цилиндра (радиусом

и высотой

). Объем такого тела равен:



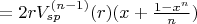
Обозначим

Тогда

Примечания:
а) Конечно, "пилить" надо аккуратно, чтобы "не задеть" лежащий внутри тела шар. Для этого надо брать

(что понятно из простейших геометрических соображений).
б) Такое преобразование описанного тела имеет смысл при

.
При таких ограничениях можно подобрать такие значения

, что

Для этих значений x

Однако

(шар лежит внутри тела), поэтому

(в случае

).
Таким образом, при увеличении размерности на 1 объем шара уменьшается в некоторое число раз, большее 1 (адаптированное объяснение школьнику: очередной элемент последовательности объемов шаров не превышает соответствующего элемента бесконечно убывающей геометрической прогрессии). Очевидно, что последовательность объемов шаров с увеличивающейся размерностью имеет своим пределом 0.
Увы, изяществом "доказательство" не блещет. Зато школьнику может быть понятно.