Вероятность возникновения тупоугольного треугольника

[Лукомор]

Alex1976 в сообщении #204835 писал(а):

Почти угадали, примерно 0,64 ( 0.5*pi/(1,(3)*pi - sqrt(3)).

А я не угадывал, я считал по методу предложенному PAV:

PAV в сообщении #204749 писал(а):

Давайте разберемся. Сначала рассмотрим второй способ построения, при котором точка бросается в область. Без ограничения общности будем считать, что две исходные точки расположены на координатной плоскости как $(0,0)$ и $(0,1)$. Тогда получается, что третью точку предлагается бросать в область, равную пересечению кругов с центрами в этих двух точках и имеющих радиус 1.

При этом $P=(2\pi/3-\pi/4)/(2\pi/3)=0.625$ Точно.

Добавлено спустя 25 минут 20 секунд:

Alex1976 писал(а):

Только вопрос не в том, чтобы посчитать, а в объяснении, почему одно число меньше другого.

Потому что Вы задали два разных дополнительных условия.
Соответственно получили две разных условных вероятности.

Alex1976 писал(а):

Как вариант - какой способ "больше похож" на "случайный треугольник на плоскости".

Больше похож вот этот:

gris писал(а):

Поскольку линейные размеры для нас не существены, опишем треугольник двумя углами $A$ и $B$.
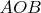
Рассмотрим квадрат в системе координат $AOB$. Каждая точка квадрата под отрезком $A+B=180$ (диагональю), будет соответствовать одному треугольнику.
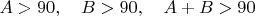
Тупоугольные треугольники будут соответствовать неравенствам $A>90,\quad B>90,\quad A+B>90$. Области, определяемые неравенствами, будут занимать $\frac34$ площади треугольника.

[Alex1976]

PAV писал(а):

Хорошо, а можете Вы объяснить для начала, "почему" если $X$ имеет равномерное распределение на отрезке $[0,1]$, то распределение $X^2$ на том же отрезке будет уже не равномерным?

Вот обсуждение и скатилось до хамства.

Раз уж Вы сами модератор, прошу либо тему закрыть, либо от хамства воздерживаться.

[PAV]

Не вижу никакого хамства. Я не понимаю, какого ответа Вы ждете. Поясните на указанном мной примере, как объяснять, "почему" при некотором преобразовании равномерное распределение переходит в неравномерное? Потому что формулы такие.

На самом деле мой пример по сути очень близок к приведенному. В нем преобразование происходит с переменным коэффициентом, поэтому области равной площади переходят в области неравной площади, поэтому и равномерность теряется. С треугольниками то же самое.

Впрочем, своим последним постом вы производите на меня впечатление не вполне адекватного человека, поэтому я дальше здесь ничего обсуждать не собираюсь. Счастливо оставаться, разбирайтесь со своими вопросами сами.

[Мат]

Alex1976
А разве обе точки не будут лежать на прямой $[0; 1]$?

[Лукомор]

Лукомор в сообщении #204991 писал(а):

Alex1976 писал(а):

Как вариант - какой способ "больше похож" на "случайный треугольник на плоскости".

Есть еще способ построить "случайный треугольник на плоскости".
Кидаем на плоскость три случайных точки.
Поскольку через три точки можно всегда провести окружность, то выбираем окружность единичного радиуса, на окружность кидаем три случайные точки и соединяем их прямыми.
Получаем "случайный треугольник на плоскости".
Вероятность того, что он тупоугольный: $P=3/4$.