Недавно попалось на глаза собрание сочинений Декарта, где в "Правилах для руководства ума", наряду с рассуждениями на тему изображения площади прямоугольника в виде длины линии, в неявном виде был поставлен эксперимент, который до Декарта не приходил никому в голову...
Объем куба (куб) произвольной величины можно получить путем перемножения трех отрезков произвольной, но одинаковой длины друг на друга:

, отложенных по определенному правилу (перпендикулярно друг другу) из одной точки
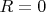
.
А можно получить этот же куб (объем куба) путем сложения трех пирамид, с вешинами, находящимися в одной общей точке
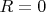
:
http://www.korthalsaltes.com/three_py...a_cube.htm
(если не "откроется", пройти по: Pyramids-Three pyramids in a Cube)

и разделенных друг от друга тремя площадями

).
Суть эксперимента состояла в следующем:
"Разбить" куб (объем куба) на две части

и, изобразив объем куба в виде площади прямоугольника (ширина

и длина

), посмотреть, в виде чего в этом прямоугольнике будут выглядеть три пирамиды и площади!
Эксперимент проводился следующим образом:
1. По горизонтали, на оси

откладывались одна за другой все увеличивающиеся (произвольно) по длине ширины (

...) прямоугольников,
2. По вертикали, на оси

откладывались одна за другой соответствующие длины длин (прошу прощение за тавтологию) (

...) соответствующих "своим ширинам" прямоугольников.
3. Затем у прямоугольников дорисовывались две оставшиеся стороны.
4. Были проведены замеры и получены следующие результаты:
- площади прямоугольников были численно равны объемам кубов (

...);
- площадь каждого прямоугольника была "разбита" на две части (

и

) некоторой воображаемой линией, получившейся, как траектория вершин прямоугольников, лежащих по диагонали от
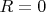
. Причем площадь

численно соответствовала объему двух пирамид (

) и была расположена "над воображаемой линией раздела". Другая часть площади прямоугольника

численно соответствовала объему третьей оставшейся пирамиды и была расположена "под воображаемой линией раздела";
-воображаемая линия раздела двух площадей (

и

) численно не совпадала с площадью

вследствии своего искажения, т.к. все-таки куб - не прямоугольник.
Убедившись, после еще нескольких измерений, в абсурдном противоречии здравому смыслу результатов поиска других соответствий, Декарт спрятал результаты своего опыта подальше в архив.
P.S. Очевидно, что после его смерти ученики Декарта все-таки "откопали" черновики этого эксперимента...



