По-видимому, в разных источниках описаны разные алгоритмы Миллера или я что-то недопонимаю

Как я представляю себе детерминированный вариант теста Миллера-Рабина (алгоритм Миллера).
Согласно этого алгоритма первым делом выясняется степень четности

числа

, где
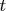
- нечетное.
Следующее - необходимо проверить первое число

на выполнение сравнения

.
Если сравнение выполняется, то переходят к следующему

(предварительно проверив делимость

на

).
В противном случае (т.е. сравнение не выполняется) далее проверяют

, если это сравнение выполняется, то переходят к следующему

,
если не выполняется, то проверяют выполнение следующего сравнения

и так до

.
Если и последнее сравнение не выполняется, то число объявляется "составным".
Согласно алгоритма Миллера, если число прошло проверку при

от 2 до

, то в случае выполнения обобщенной гипотезы Римана можно сделать вывод - "число простое".
Например,

;

, следовательно,

;

.
Принимаем

.

,
следовательно, проверяем:





,
делаем вывод: число

- составное.
Добавлено спустя 27 минут 35 секунд:
Если мое представление о тесте верное, то

- это степень четности выражения

и от

не зависит.
Добавлено спустя 43 минуты 17 секунд:
Хотя, коль скоро речь идет о максимальном значении

, то оно от логарифма зависит.
Я отдаленно понял, о чем речь. Спасибо.