открывая тему, druggist писал(а):
Для наглядности возьмем распределение массы М по оси Х. Как должна быть распределена масса, по оси, чтобы распределение было фрактальным? Функция плотности m(x) в этом случае не будет иметь производной? как это, что называется, "на пальцах" пояснить?
Как уже отмечал
AD, исходная формулировка вопроса в темы некорректна. Более корректная формулировка получится, если вместо
«Функция плотности m(x) в этом случае не будет иметь производной?»,
записать
«Функция распределения массы
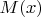
в этом случае не будет иметь плотность?».
Постараюсь «ответить» на так поставленный вопрос.
1. Как уже было отмечено выше, интересующее распределение массы связано с понятием Канторового множества. Научно-популярное изложение построения распределения массы, не имеющего плотность, приводится в [1, c.73].
Цитата:
Будем считать затравкой не единичный отрезок, а стержень из какого-нибудь материала с плотностью

. Исходный стержень имеет длину

, и, следовательно, массу

. Операция, связывания с применением образующего элемента, состоит из разрезания стержня на две половины равной массы

, которые затем в результате ковки укорачиваются до длины

(одинаковой для обеих половинок). В результате такой обработки плотность возрастает до

. Повторяя всю процедуру, мы получим в n-ом поколении

маленьких стержней, каждый из которых имеет длину

и массу

при

. Заметим, что масса в ходе обработки сохраняется, поэтому

…
Из сказанного следует, что масса отрезка длиной

, где

определяется выражением

.
Скейлинговый показатель здесь равен

. Плотность каждого из малых отрезков стержня определяется выражением

и расходится при

.
2. По поводу желания рассмотреть явление на простом примере конечного множества точек.
Цитата:
Мне не хотелось бы рассматривать непрерывный отрезок. Для конкретности пусть будет М частиц, шаров и,т.д., которые можно разместить по N местам, корзинам и пр. При этом даже не надо, чтобы они(корзины) равномерно располагались по оси х, достаточно того, что их можно было перенумеровать. Пусть m(i) - размер i-той кучки, или число частиц m в состоянии i, плотность есть отношение дельта M к дельта i, число частиц, заключенных в корзинках под номерами от i до i+дельта i . Правильно ли я понимаю ситуацию: если для любого i дельта M линейно зависит от дельта i , то имеем однородное распределение с постоянной плотностью, а если не линейно имеем фрактальное распределение?
В этом случае функция распределение массы будет предсталять «ступечатую» функцию:

,
где индикатор

определяется так:

. [Такая функция распределения массы,
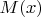
, испытывает скачки величиной

в точках

.] Для дискретного случая также нельзя ввести плотность. Т.е. не найдется такой функции

, что

. Кроме того, множество изолированных точек, которым Вы приписываете, массы

имеет топологическую размерность равную нулю и размерность Хаусдорфа—Безиковича равную нулю, а фрактал — это множество, у которого размерность Хаусдорфа—Безиковича строго больше его топологической размерности. Т.е. конечное множество точек в качестве иллюстрации отсутсвия у фрактала плотности — заведомо не годится.
Ref.
[1] Федер Е. Фракталы. — М.: Мир, 1991.



