Нужно воспользоваться теоремой Пикара и оценками, полученными в ходе ее доказательства (см. например Н.М. Матвеев, Методы интегрирования обыкновенных дифференциальных уравнений). По теореме Пикара если

непрерывна в области

,

, причем в этой области

,

, то решение уравнения


с начальными данными

существует и единственно при

, причем

.
В процессе доказательства решение строится в виде суммы ряда

, где

- приближения, которые вы строите в процессе вашего решения. Для доказательства его сходимости выводится оценка

.
Откуда получаем оценку для

-го приближения:

,



.
В вашем случае
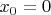
,

,

. Очевидно,

,

. Нужно подобрать

так, чтобы решение существовало на

, т.е.

и воспользоваться оценкой выше.



