maxal писал(а):
Элементы группы 12-го порядка - это выражения вида

(или с нижними индексами вместо верхних как у Холла),где

может принимать значения от

до

, а

или

(причем

и

могут быть опущены в произведении). Здесь абсолютно неважно, чему конкретно равны

и

, важно только что степень

всегда берется по модулю 6, а степень

- по модулю 2. Таким образом, существует ровно 12 различных элементов вида

.
Ничего не поняла!
Во-первых, нижний индекс - это индекс, а показатель степени (как у вас написано) - это показатель степени. Так как же понимать выражение

? В нём

и

индексы или показатели степени?
Перед тем, как разбираться с построением Холла, я, конечно, открыла Википедию и посмотрела, что такое абелева группа. Однако ни по описанию, данному Холлом, ни по вашему описанию я не могу составить абелеву группу 12-го порядка, состоящую из 12 различных элементов, таких, что для некоторой бинарной операции в этой группе для любых элементов

и

, принадлежащих данной группе, верно:
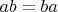
. Именно так я поняла по определению, данному в Википедии, абелеву группу.
Давайте конкретно, без символов и без индексов: какие 12 различных элементов составляют абелеву группу 12 порядка, из которых можно строить ортогональные латинские квадраты 12-го порядка? Как далее составить из этих элементов 5 строк? Что далее делать с элементами этих строк? Покажите, пожалуйста, хотя бы пару ОЛК 12-го порядка, построенную таким способом.
Вот, например, по вашему описанию я пишу 12 различных элементов абелевой группы 12-го порядка:

Это правильные элементы? Я понимаю здесь

и

как показатели степени. Но когда я беру произвольные числовые значения, у меня получается ерунда какая-то, а не абелева группа.