Наконец-то начали поступать решения задач 11-го тура.
Может быть, следовало еще немного подождать с разбором, чтобы решений стало побольше...
Но, боюсь, при таком развитии событий участники Марафона совсем перестанут реагировать на сроки приема решений, ожидая очередного их продления. Поэтому я решил таки опубликовать разбор задач ММ101-ММ104.
================Баллы, полученные за решение задачи 101 учитываются дважды: в основном Марафоне и в тематическом конкурсе.
Задача 101 является прямым продолжением задачи ММ57.
ММ101 (КГ-1) (8 баллов)
Назовем многоугольник ординарным, если он выпуклый и никакие 3 его диагонали не пересекаются в одной точке внутри многоугольника. Пусть n - число сторон ординарного многоугольника. Ординарный многоугольник разбивается своими диагоналями на многоугольники, которые мы будем называть элементарными.
Начиная с какого n, число элементарных четырехугольников может превысить число элементарных треугольников?
РешениеПри n = 9 требуемым многоугольником будет, например, девятиугольник с вершинами

. В его разбиении участвуют 67 треугольников, 69 четырехугольников и 18 пятиугольников.
Остается показать, что при n < 9 в разбиении ординарнрого (да и любого выпуклого) n-угольника треугольников больше, чем четырехугольников.
Для n < 8 это очевидно.
Пусть n = 8.
Своими диагоналями ординарный восьмиугольник разбивается на 91 часть (обоснование можно посмотреть в разборе задачи ММ57). 40 элементарных многоугольников, имеющих общую вершину с исходным многоугольником, являются треугольниками. На остальные 51 элементарных многоугольников приходится 208
углов, что пока не исключает возможности превышения четырехугольников над треугольниками.
Зафиксируем одну вершину исходного восьмиугольника вместе со смежными ей сторонами и диагоналями. Остальные вершины, стороны и диагонали образуют ординарный семиугольник. Среди элементарных многоугольников этого семиугольника 28 треугольников, имеющих общую вершину с исходным семиугольником. Возможные количества углов остальных 22 элементарных многоугольников представлены в приведенной ниже таблице (обоснование этой таблицы см. в разборе решения задачи ММ104):

Диагонали, проведенные из зафиксированной нами восьмой вершины, разрежут некоторые из частей разбиения. Однако, при разрезании треугольной части обязательно вновь возникнет треугольник, а разрезании пяти(или более)угольной части возникнет хотя один элементарный многоугольник, имеющий не менее 5 сторон. Поэтому среди 51 части в разбиении восьмиугольника, возникающего на пересечении коротких (соединяющих вершины через одну) диагоналей исходного, будет не менее 3 треугольников и не менее 6 элементарных многоугольников, имеющих боле четырех сторон.
Окончательно получаем, что в разбиении ординарного восьмиугольника участвует не менее 43 треугольников. Из 48 оставшихся многоугольников не менее 6 имеют более четырех сторон.
ОбсуждениеОценки (не менее 43 треугольников и не менее 6 элементарных многоугольников с числом сторон более четырех), вполне достаточны для решения данной задачи, но, скорее всего, занижены.
Участники конкурса привели еще несколько примеров девятиугольников, у которых среди частей разбиения больше четырехугольников, чем треугольников. Анатолий Казмерчук нашел девятиугольник, в разбиении которого участвуют 66 треугольников и 71 четырехугольник, а Андрей Халявин обнаружил девятиугольник, у которого всего 64 элементарных треугольника и целых 75 элементарных четырехугольников.
В преамбуле к задаче я рекомендовал, приступая к ее решению, познакомиться с разбором задачи ММ57. Но сам же пренебрег этим советом. Мне казалось, что в ММ57 обоснованы все возможные варианты разбиения ординарнрго семиугольника. Знание этих вариантов значительно упрощает решение ММ101. Поэтому первоначально данная задача была оценена всего в 5 баллов.
НаградыЗа правильное решение задачи №101 Андрей Халявин получает 9 призовых баллов (1 балл добавлен за оперативность реакции), а Анатолий Казмерчук - 8 баллов. Кирилл Веденский получает 2 призовых балла, а Николай Дерюгин - 1.
Эстетическая оценка задачи - 5 баллов=============== Баллы, полученные за решение данной задачи учитываются дважды: в основном Марафоне и в тематическом конкурсе. А сама задача тесно связана с задачами ММ57, ММ101 и ММ104.
ММ102 (КГ-2) (9 баллов)
На какое наименьшее число частей может разбиваться диагоналями выпуклый n-угольник
при:
a) n = 6;
b) n = 7;
c) n = 8;
d) n = 9?
Примечание:
Цена задачи указана весьма условно.
Я умею строго обосновывать минимальность известных мне разбиений не для всех указанных n. Cоответственно и сами известные мне ответы могут оказаться неверными. 9 призовых баллов будет присуждаться за решения аналогичные моему (имеющие тот же ответ и ту же степень строгости его обоснования). За улучшение известных мне ответов, получение более строгих обоснований, получение
(хотя бы частично) обоснованных ответов для бОльших n будут начисляться дополнительные призовые баллы.
РешениеБудем называть диагонали, соединяющие вершины выпуклого многоугольника через одну "короткими"), через две - "средними", через три - "длинными". Точку внутри многоугольника будем называть особенностью порядка

, если в ней пересекаются

диагоналей. Ясно, что особые точки могут возникать только при пересечении средних и длинных диагоналей.
Ординарный n-угольник разбивается своими диагоналями на

частей, что при интересующих нас n составляет 25, 50, 91 и 154 соответственно. Каждая особенность порядка k уменьшает количество частей разбиения на

. Сумму этих чисел по всем особенностям будем называть дефектом многоугольника. Для решения задачи нужно найти максимальный дефект для каждого из данных n.
a) У шестиугольника всего 3 диагонали, не являющихся короткими. Поэтому в шестиугольнике может возникнуть всего одна особенность порядка 1 (она есть, например, в правильном шестиугольнике). Соответственно максимальный возможный дефект шестиугольника - 1 и минимально возможное число частей разбиения - 24.
b) У семиугольника не может быть особенностей, порядок которых больше 1, (вершин не хватает). А то, что число особенностей первого порядка не может превышать 3, следует из рассуждений, приведенных в решении задачи ММ104. В то же время 3 особых точки возможны. На рисунке 1 приведены два способа получения семиугольника с тремя особыми точками: достроением правильного пятиугольника; удалением вершины
правильного восьмиугольника. Разумеется, существуют и подходящие семиугольники никак не связанные с правильными многоугольниками. Итак, максимальный дефект семиугольника - 3, наименьшее возможное число частей разбиения - 47.
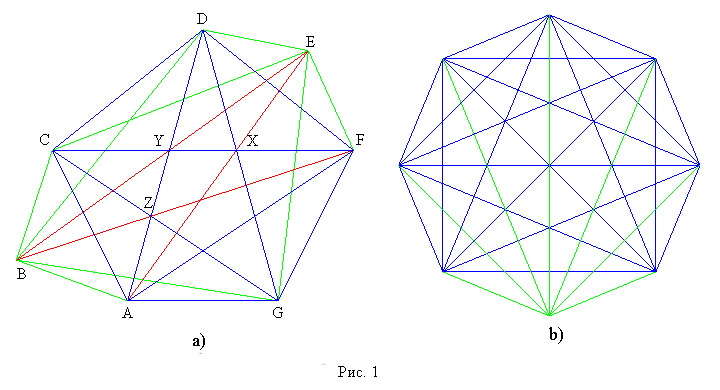
c) Представляется очевидным, что максимальный возможный дефект восьмиугольника возникает (в частности) у правильного восьмиугольника. Докажем это утверждение. При наличии особенности второго порядка на средней диагонали не может быть больше двух особенностей. Это легко увидеть на рисунке 2.

На средней диагонали 1-4 уже есть две особенности Y и V. Точки пересечения нашей диагонали с короткими диагоналями не могут быть особенными. Остаются два кандидата на особые точки. Это X и U. Cделать точку X особой можно за счет смещения диагонали 3-8. Но это неизбежно приведет к тому, что точка Y, а заодно и Z перестанут особыми. Аналогично обстоят дела с точкой V. Поэтому на средней диагонали восьмиугольника не может быть больше двух особых точек. Но
у правильного восьмиугольника на каждой средней диагонали их ровно по две. Единственная особенность второго порядка может возникать только на пересечении всех длинных диагоналей восьмиугольника. И у правильного восьмиугольника такая особенность есть.
Таким образом, правильный восьмиугольник обладает максимальным дефектом среди всех восьмиугольников: он имеет 8 особых точек первого порядка и одну особую точку второго порядка. Поэтому дефект правильного восьмиугольника - 11, а число частей разбиения 80.
d) Именно к этому пункту относилось примечание к условию. Мне удалось найти девятигольник с дефектом 17. Я полагаю, что это максимальный возможный дефект, но доказывать это не умею.
Как и все конкурсанты, бравшиеся за задачу ММ102, я стартовал с правильного восьмиугольника. Поместим вершины правильного восьмиугольника на единичной окружности, в точках с координатами

, где

. В качестве девятой вершины возьмем точку с координатами

(она тоже лежит на
единичной окружности). Не сложно убедиться, что жирные синие точки на рисунке 3 являются особыми, а две наиболее крупные из них - особенности второго порядка.

Поэтому дефект нашего девятиугольника равен 17, а число частей разбиения - 137.
ОбсуждениеПредставляется правдоподобной гипотеза: при четных n максимальный дефект имеют правильные n-угольники. Другое утверждение "правильные n-угольники с нечетным числом сторон ординарны" относительно недавно перекочевало из разряда правдоподобных предположений в категорию теорем. Набросок доказательства появился еще в 1936 году в статье G.Bol: Beantwoording van prijsvraag no.17,
Nieuw Archief voor WisKunde 18 (1936), p.14-66. Но строгое доказательство было опубликовано лишь в 1998 году: см. "The number of intersection points made by the diagonals of a regular polygon", B. Poonen, M. Rubinstein, SIAM J. on Discrete Mathematics, Vol. 11, No. 1 (1998), p. 135-156.
В этой статье выведена формула для количества частей разбиения правильного n-угольника при любом n. Оказывается, за исключением центра, никакая особенность правильного n-угольника не может иметь порядок выше 5, а особенности пятого порядка (отличные от центра) впервые встречается в правильном 30-угольнике. В целом же формула для числа частей разбиения распадается на 2520 случаев (которые авторам не без изящества удалось запихнуть в одну не слишком громоздкую формулу).
Если принять гипотезу о том, что правильный десятиугольник - "наиболее дефективный" среди десятиугольников, можно получить еще одно косвенное подтверждение тому, что построенный нами девятиугольник имеет максимальный возможный дефект. Добавив к нашему девятиугольнику вершину, cимметричную девятой вершине относительно центра исходного восьмиугольника (см. рис. 4),
получим десятиугольник с дефектом 26, т.е. с таким же дефектом. как у правильного десятиугольника.

Андрей Халявин нашел для дефекта девятиугольника некоторую оценку сверку. Но она безусловно сильно завышена (28).
Анатолий Казмерчук тоже нашел было девятиугольник с дефектом 17, но при ближайшем рассмотрении этот объект оказался то ли не совсем выпуклым, то ли не совсем девятиугольником (см. рис. 5).
 Награды
НаградыАндрей Халявин и Анатолий Казмерчук (нашедшие девятиугольники с дефеком 15) получают по 8 призовых баллов. Николай Дерюгин нарисовал девятиугольник разрезаный 137 частей и поразительно похожий на тот, что приведен на рисунке 3 (только красиво раскрашенный), но не снабдил свою картинку обоснованиями (более строгими чем "похоже, что..."). Кроме того, он не обосновал максимальность дефекта правильного восьмиугольника. Николай получает 6 призовых баллов.
Эстетическая оценка задачи - 5 баллов================Баллы, полученные за решение данной задачи учитываются дважды: в основном Марафоне и в тематическом конкурсе. А сама задача является прямым продолжением задач ММ57, ММ101 и ММ102.
ММ103 (КГ-3) (3 балла)
Сопоставим каждому выпуклому многоугольнику (сопровождающий) граф по следующему правилу:
вершинами графа будут элементарные многоугольники;
две вершины смежны, если соответствующие многоугольники имеют общую сторону.
1. Доказать, что сопровождающий граф любого выпуклого многоугольника является планарным и двудольным.
2. Сформулировать условие ординарности многоугольника в терминах сопровождающего графа.
РешениеПланарность сопровождающего графа доказывается просто (ведь, по сути он уже уложен на плоскость). Внутри каждого элементарного многоугольника выбирается точка, изображающая вершину графа. Точки, лежащие в областях, имеющих общую сторону, соединяются непересекающимися линиями, лежащими целиком внутри данных смежных элементарных многоугольников.
Двудольность сопровождающего графа легко доказать по индукции. Проведем сначала одну диагональ. Исходный многоугольник разобьется на два, которые можно выкрасить в разные цвета. Остается заметить, что добавление диагонали не лишает нас возможности правильно (чтобы смежные многоугольники были окрашены в разные цвета) раскрасить многоугольники разбиения в два цвета. Для этого достаточно инвертировать цвета всех многоугольников разбиения по одну сторону од добавляемой диагонали.
НаградыЭстетическая оценка задачи - 4 балла================Баллы, полученные за решение данной задачи учитываются дважды: в основном Марафоне и в тематическом конкурсе. А сама задача является прямым продолжением задач ММ57, ММ101, ММ102 и ММ103.
ММ104 (КГ-4) (9 баллов)
Два ординарных n-угольника назовем изоморфными, если изоморфны их сопровождающие графы (см. ММ103).
Два ординарных n-угольника назовем однотипными, если в разбиениях этих многоугольников на элементарные присутствует поровну треугольников, поровну четырехугольников и т.д.
1. Имеется ли логическая зависимость между однотипностью и изоморфностью ординарных многоугольников?
2. На сколько классов однотипных семиугольников разбиваются ординарные семиугольники?
3. На сколько классов изоморфных семиугольников разбиваются ординарные семиугольники?
Решение1. Очевидно, что и однотипность и изоморфность являются отношениями эквивалентности на множестве ординарных n-угольников. Степень каждой вершины сопровождающего графа равна количеству сторон соответствующего элементарного многоугольника (исключение составляют n элементарных треугольников, у которых одна из сторон является стороной исходного n-угольника). Поскольку степени соответствующих вершин изоморфных графов равны, очевидно, что изоморфные многоугольники являются одновременно и однотипными. То, что обратное утверждение не имеет места будет видно из рассмотрения последующих пунктов.
2-3. Диагонали выпуклого семиугольника, соединяющие вершины через одну, будем называть "короткими", а остальные - "длинными". На рисунках короткие диагонали изображены зеленым цветом, а длинные - красным. Короткие диагонали высекают из исходного семиугольника внутренний семиугольник, содержащий 22 элементарных многоугольника (эти элементарные многоугольники, а также точки пересечения длинных диагоналей мы тоже будем называть внутренними). Остальные 28 элементарных многоугольников (будем называть образованную ими часть семиугольника "периферийной") для любого ординарного (и даже для любого выпуклого) семиугольника являются треугольниками. Строение периферийной части одинаково для всех выпуклых семиугольников. Учитывая это, договоримся при изображении сопровождающего графа, рисовать только 22-вершинный подграф, порожденный внутренними элементарными многоугольниками. (В то же время, исходные семиугольники будем рисовать целиком.)
Стартуем с рассмотрения семиугольника, изоморфного (а значит, и однотипного) правильному. Он изображен на рисунке 1, а внутренняя часть его сопровождающего графа - на рисунке 2 (голубым цветом изображены вершины, соответствующие треугольникам; зеленые - четырехугольникам; желтые - пятиугольникам; красная - семиугольнику).


Пронумеруем вершины семиугольника и введем обозначения для точек пересечения длинных диагоналей: А - на пересечении диагоналей 1-4 и 2-6 и т.д. (см. рисунок). Те из внутренних точек, которые являются вершинами элементарного семиугольника, дополнительно будем называть "центральными", а остальные внутренние точки - "окаймляющими".
Деформируя наш семиугольник, мы можем поменять строение сопровождающего графа только за счет изменения взаимного расположения внутренних точек. Например, смещая вершины 3 и/или 7, можно добиться, чтобы диагональ 3-7 оказалась по другую сторону от точки A. Аналогичного эффекта можно добиться для других окаймляющих точек. Но некоторые такие "перетаскивания" несовместимы. Если мы перетаскиваем соответствующую диагональ за одну из окаймляющих точек, то мы не можем проделать то же самое с соседними окаймляющими точками. Так, перетаскивая диагональ 3-7 за точку A, мы лишаем себя возможности, перетащить диагональ 1-4 за точку B и диагональ 2-6 за точку G. Поэтому элементарный семиугольник можно лишить не более чем трех вершин.
Учитывая вышеизложенное мы легко можем перечислить все классы изоморфных ординарных семиугольников.
1. Семиугольники, изоморфные правильному. Такой семиугольник и центральную часть его сопровождающего графа мы уже рассмотрели (рис. 1-2). У таких семиугольников разбиение состоит из 28+7 треугольников, 7 четырехугольников, 7 пятиугольников и одного семиугольника.
2. Семиугольники полученные из семиугольников первого класса перетаскиванием одной (из соображений симметрии все равно какой) длинной диагонали за окаймляющую точку. На рисунке 3 приведен семиугольник, полученный из первого, перетаскиванием диагонали 2-5 за точку C, а на рисунке 4 - центральная часть его графа. У таких семиугольников разбиение состоит из 28+5 треугольников, 10 четырехугольников, 6 пятиугольников и одного шестиугольника.


3. Семиугольники полученные из семиугольников первого класса перетаскиванием двух диагоналей за окаймляющие точки, расположенные через одну. На рисунке 5 приведен семиугольник, полученный из первого, перетаскиванием диагонали 2-5 за точку C и диагонали 3-7 за точку A. На рисунке 6 приведена внутренняя часть сопровождающего графа. У таких семиугольников разбиение состоит из 28+4 треугольников, 11 четырехугольников и 7 пятиугольников.


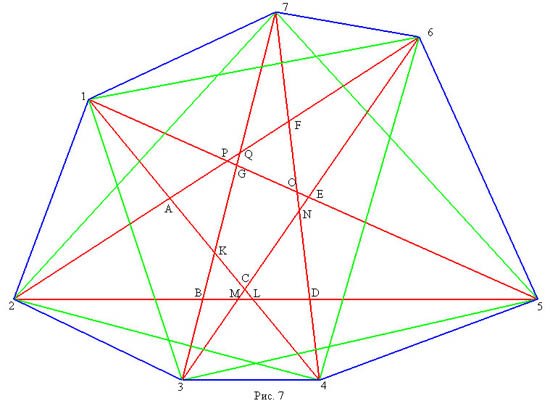
4. Семиугольники полученные из семиугольников первого класса перетаскиванием двух диагоналей за окаймляющие точки, расположенные через две. На рисунке 7 приведен семиугольник, полученный из первого, перетаскиванием диагонали 2-5 за точку C и диагонали 2-6 за точку G. На рисунке 6 приведена внутренняя часть сопровождающего графа. У таких семиугольников разбиение состоит из 28+3 треугольников, 13 четырехугольников и 6 пятиугольников.

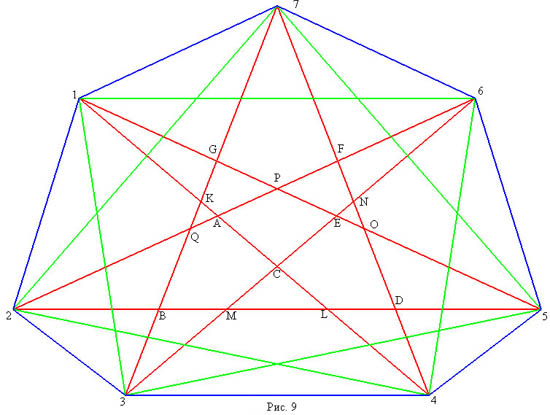
5. Семиугольники полученные из семиугольников первого класса перетаскиванием трех диагоналей за окаймляющие точки. На рисунке 9 приведен семиугольник, полученный из первого, перетаскиванием диагонали 2-5 за точку C, диагонали 3-7 за точку A и диагонали 4-7 за точку Е. Внутренняя часть сопровождающего графа приведена на рисунке 10. У таких семиугольников разбиение состоит из 28+3 треугольников, 13 четырехугольников и 6 пятиугольников.

Семиугольники из последних двух классов оказались однотипными. В то же время, их сопровождающие графы, очевидно, не изоморфны (например, у одного из них во внутренней части есть вершины степени 3, удаленные друг от друга на 2, а у другого - нет). Таким образом, имеется 5 классов изоморфных и 4 класса однотипных ординарных семиугольников.
ОбсуждениеАналогичная классификация ординарных (или любых выпуклых) n-угольников для бОльших представляется весьма трудной (хотя, по крайней мере, при

вполне посильной) задачей.
НаградыЗа правильное решение этой задачи Анатолий Казмерчук получает 9 призовых баллов.
Эстетическая оценка задачи - 5 баллов ================


