Cхема основного доказательства из Части II.Особенно будет понятной для тех, кто прошёл Часть I.

-Множества (например,

-линии,

-точки,

-функции) – это просто последовательности классических множеств (последовательности, составленные из линий, точек,функций), т.е. определённые как функции от натуральных чисел со значениями, которые суть – классические множества. Постоянные в значениях последовательности изображают классические множества, аналог классических множеств, тем «знаковосоответствуют» последним. Классические множества называем

-множествами. Можно считать, что приставка

от английского слова «последовательность».
Далее, просто пытаемся доказать аксиому I, но в «

-варианте».
Пару

-последовательностей, составленых из

-линий множества

(см. раздел III Части I, жирное каллиграфическое

в основном тексте), и определяющих сечение в множестве

, превращаем сначала в (знакосоотвествующие)

-последовательности

-линий. Множество

тогда же превращается в

-множество
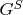
, знакосоответствующее множеству

. Все

-линии,

-принадлежащие указанным

-последовательностям, образуют

-множество

(фигурное, каллиграфическое особое

в основном тесте). В

-множестве

рассматриваем только его

-конечные

-части (в грубом приближении этого пояснения – конечные для каждого значения-элемента такой

-части, т.е. для элемента последовательности, трактуемого как конечная часть классического множества линий). Эти

-конечные

-части пытаемся сопоставить с другими

-конечными

-множествами. Если снять приставки

-, то последнее означает, что линиии какого-нибудь конечного множества просто совмещаем с линиями некоего другого конечного множества так, чтобы линии совпали, но сохранилось бы их взаимное расположение (топология), и совмещение производим посредством непрерывного отображения плоскости на себя (названного «предсопоставлением»).
Если снять приставки

-, (трактовать события так, как о них думает

-теоретик) то делаем дубликат той оригинальной плоскости, на которой расположены сопоставляемые линии множества

, взятые из множества

(на самом деле корректно говорить об

-множествах). И сопоставляем линии из

оригинальной плоскости линиям дубликата. Строго говоря,

-сопоставляем

-линии

-множества

некоторым

-линиям

.
Для того, заранее выбираем некую (не меняемую в рассуждениях «

-константу»)

-линию

, т.е. вообще говоря, переменную

-линию, положения

которой совпадают с классическими линиями

и зависят от натурального аргумента



. Каждое сопоставляемое

-конечное

-множество

делим (условно для этого пояснения, и такое обозначение весьма отличается от обозначения основного текста) на непересекающиеся друг с другом «правое»

и «левое»
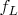
,

-объединение которых и есть

. В частности, такое означает, что для каждого



(если рассуждать грубо, точнее же, для каждого натурального

из множества, принадлежащего ультрафильтру, определяющему теорию

), все линии из


асимптотически завершаются на дуге

(см. Часть I, раздел III, в основном тексте это обозначение

с нижним фигурным штрихом) правее линии

, и все линии из
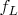

асимптотически завершаются на дуге

левее линии

.
В результате, строим, определяем трансфинитную

-последовательность

-конечных

-сопоставлений, нумерованных ординалами


.

-Сопоставления с болЬшими номерами


(точнее, значения этих

-сопоставлений как функций от аргумента



) для всех достаточно больших



«включают в себя»

-сопоставления с меньшими номарами


. В таком определении трансфинитной цепочки

-сопоставлений активно пользуемся гипотезой Кантора, т.е. их,

-сопоставлений, предполагаем, всего «алеф-один».
Если бы подобные попытки сопоставлений делались с обычными, классическими множествами, то надо было бы как-то обосновать появление линии

, но последнее и есть доказываемое утверждение. Т.е. тогда приходим к некоему кругу трудностей. Но для

-сопоставлений такая линия (точнее

-линия) определима тривиально заранее. Т.е. после того, как её ввели, к указанной трансфинитной последовательности, добавляем одну за другой - добавляем к счётному множеству уже

-сопоставленных

-линий - новые

-сопоставляемые

-линии, взятые из «дубликата» –

-сопоставляемые

-линиям «оригинала» из указанной пары последовательностей.
В результате, доказуемо существование

-ультрафильтра, составленного из

-сопоставлений, или из

-ординалов (как в основном тексте), которые суть

-номера таких

-сопоставлений. Этот

-ультрафильтр таков, что если

-линия

-принадлежит

-множеству

, то найдётся множество

-сопоставлений из указанного

-ультрафильтра, каждое из которых,

-сопоставляет эту

-линию какой-то

-линии дубликата. Если же

-сопоставляются две такие

-линии, то подобно же

-сопоставляются и их

-точки

-пересечений. Потому, существует единое

-предсопоставление, которое

-сопоставляет

-линии из

некоему аналогичному

-множеству

-линий

, взятых из дубликата (последние обозначения сильно разнятся с теми, что в основном тексте). А

-линии из

и

-линия

располагаются также, как это требует аксиома I (точнее, знаковосоответствующий

-аналог такой аксиомы). Поскольку из аксиомы I следует нарушение континуум-гипотезы, то получаем, что либо канторова гипотеза не верна, либо верна аксиома I. Т.е. получаем утверждение, похожее на аксиому I, но, вообще говоря, получаем пока не более чем простое нарушение континуум-гипотезы.
Почему применена каллиграфия? Буквенных шаблонных обозначений катастрафически не хватает для того, чтобы не возникало коллизий, и не приходилось бы каждый раз обозначать одной буквой весьма разные предметы, и затем объяснять, что имелось ввиду в этот раз, а не в другие разы. Обычные штрихи, звёздочки и индексы оказываются весьма примитивным инструментом, и не спасают положение. Потому, кажется правильным применять по сути иероглифы, которые как рисунки в большей степени отражают нюансы мысли. Например, «фигурные штрихи», «стилизованные буквы». Строго говоря, любые шаблоны сильно ограничивают выражение мысли (Написание от руки оказывается более совершенным способом нанесения знаков для выражения мысли, чем применение машинных или типографских шаблонов).
В части II увидел погрешность в итоговом доказательстве – почему-то не оговорил, что фильтру должны принадлежать, конечно, не только все конечные пересечения, но и надмножества его элементов. Исправил пару опечаток, аккуратнее дал пояснения. Потому, смотрите исправленный вариант части II по адресу:
https://vk.com/s/v1/doc/OnUFgLzIsKB0zj3 ... PFmVZAbfnI