Точное количество кортежей из простых чисел в интервале

[Yadryara]

vicvolf в сообщении #1689973 писал(а):

Я объяснил почему 0,51 и 0,33, т.е. меньше мат. ожидания выше в теме.

Может мы друг друга не понимаем? 0.51 и 0.33 — это и есть матожидания в штуках. В первом случае найдено 0 штук, то есть меньше мат. ожидания, а во втором — 1 штука, то есть больше мат. ожидания. Были полностью проверены оба диапазона.

[vicvolf]

Yadryara в сообщении #1689974 писал(а):

Может мы друг друга не понимаем?

Вы хотите получить более точный инструмент прогноза появления кортежа определенной структуры, чем HL1. Я предлагаю новый инструмент -определение расстояния между кортежами. Прогнозировать это расстояние можно более точно, так как нам известен закон его распределения. Можно подсчитать не только среднее значение, но и другие моменты и вероятность нахождения кортежа на интервале. Я не уверен, что сам прогноз через расстояния будет более точным, но если хотите....

[Yadryara]

vicvolf в сообщении #1689975 писал(а):

Я предлагаю новый инструмент -определение расстояния между кортежами.

Этот инструмент уже готов? Как с его помощью считать? Посчитайте какие-нибудь расстояния для примера, пожалуйста. Возьмите хотя бы тот же паттерн 13-168. Если сложно, тогда 3-12.

vicvolf в сообщении #1689975 писал(а):

Я не уверен, что сам прогноз через расстояния будет более точным, но если хотите....

Конечно это интересно.

[Dmitriy40]

Насколько я понял, все математические результаты тут лишь про грязные кортежи, т.е. необязательно из последовательных простых. Это конечно тоже интересно, но не надо путать чистые и грязные кортежи (и их мат.ожидания).

[Yadryara]

Чтобы не было путаницы я как раз предлагал посмотреть на сверхплотные кортежи-кристаллы. Которые по определению чистые.

[vicvolf]

Dmitriy40 в сообщении #1689991 писал(а):

Насколько я понял, все математические результаты тут лишь про грязные кортежи, т.е. необязательно из последовательных простых. Это конечно тоже интересно, но не надо путать чистые и грязные кортежи (и их мат.ожидания).

Рассматриваются допустимые кортежи, состоящие только из простых чисел. Имеется возможность определить не только мат. ожидания расстояния между простыми кортежами, но и моменты более высоких порядков, а также вероятности попадания в заданный интервал.

Yadryara в сообщении #1689998 писал(а):

Чтобы не было путаницы я как раз предлагал посмотреть на сверхплотные кортежи-кристаллы. Которые по определению чистые.

Да, для них можно определить, тем более там указано размещение 1 и 2 ого кортежей, т.е. имеется реальное расстояние. Можно проверить на восьмерках. Напишите мне $C_8$ для этих восьмерок в порядке указанном в таблице, чтобы не искать.

[vicvolf]

vicvolf в сообщении #1690051 писал(а):

Напишите мне $C_8$ для этих восьмерок в порядке указанном в таблице, чтобы не искать.

Результат для кортежа $ [0, 2, 6, 8, 12, 18, 20, 26]$: Размер кортежа $k = 8$ Константа $178.261984$
Результат для кортежа $ [0, 2, 6, 12, 14, 20, 24, 26]$:Размер кортежа $k = 8$ Константа $ 475.365290$
Результат для кортежа $ [0, 6, 8, 14, 18, 20, 24, 26]$: Размер кортежа $k = 8$ Константа $178.261984$
Верно?

[Yadryara]

vicvolf в сообщении #1690051 писал(а):

Напишите мне $C_8$ для этих восьмерок в порядке указанном в таблице, чтобы не искать.

Только сейчас заметил эту фразу. До редактирования её не было.

Но для кристаллов нет никакой C8, ведь C8 возникает аж при 8-кратном загрязнении, то есть 8-ю простыми числами. Для кристаллов есть только C0.

Ваши значения проверю попозже.

-- 12.06.2025, 21:21 --

vicvolf в сообщении #1690104 писал(а):

Результат для кортежа $ [0, 2, 6, 8, 12, 18, 20, 26]$: Размер кортежа $k = 8$ Константа $178.261984$

Что за размер такой. Надеялся, что уже давно устаканилась терминология. Длина $len = 8$.

Значения всё же отличаются:

v = [0, 2, 6,  8, 12, 18, 20, 26]; C0 = 178.2619543965
v = [0, 2, 6, 12, 14, 20, 24, 26]; C0 = 475.3652117241 
v = [0, 6, 8, 14, 18, 20, 24, 26]; C0 = 178.2619543965

[Yadryara]

vicvolf в сообщении #1690051 писал(а):

Напишите мне $C_8$ для этих восьмерок в порядке указанном в таблице, чтобы не искать.

Вот я как раз об этом спрашивал, умеете ли Вы считать константы для HL1. C0 как раз считать проще всего. Вы их где-то нашли или сами посчитали? Надо бы разобраться почему расхождения с моими подсчётами:

У Вас:  178.2619 84
У меня: 178.2619 54

У Вас:  475.3652 90
У меня: 475.3652 12

Искать-то несложно вроде.

Вот здесь они есть в самой правой колонке. И, кстати, совпадают с моими.

[Yadryara]

vicvolf в сообщении #1689975 писал(а):

Вы хотите получить более точный инструмент прогноза появления кортежа определенной структуры, чем HL1.

И никакого другого способа, кроме как научиться лучше работать с дзета-нулями — не вижу.

Где сумма по нулям большая и положительная — там и кортежей в среднем больше. Так?

Но это очень грубо, а как посчитать точнее? Я конечно могу попытаться Платту написать или ещё кому. Сказать, что мы не совсем новички в кортежных делах, рекорды показать, оценки. Может он и ответит (на чистом русском ) : Антоха, мол, начинай считать вот так, а дальше разберётесь.

Вот люди посчитали (первое?) Литлвудово нарушение на высоте $1.39716\cdot10^{316}$ Ясно, что раз там простых чисел полно, то и кортежей из них в среднем больше. Такая огромная высота конечно не нужна, но принцип счёта неплохо бы понять.

[vicvolf]

Yadryara в сообщении #1690157 писал(а):

Вот я как раз об этом спрашивал, умеете ли Вы считать константы для HL1. C0 как раз считать проще всего. Вы их где-то нашли или сами посчитали? Надо бы разобраться почему расхождения с моими подсчётами

У меня есть программа, которая считает эти постоянные с заданной точностью, т.е. она учитывает остатки от простых до определенной величины. В данном случае я взял простые до $10^8$. Можно взять больше. Все зависит от требуемой точности.

[Yadryara]

Ну вот видите, даже мы, русскоязычные люди не понимаем друг друга.

vicvolf в сообщении #1690175 писал(а):

она учитывает остатки от простых до определенной величины.

Что это значит? От всех простых? Как именно учитывает?

Yadryara в сообщении #1690166 писал(а):

Вот люди посчитали (первое?) Литлвудово нарушение на высоте $1.39716\cdot10^{316}$

А до этого в книге Дербишира было указано число $1.39822\cdot10^{316}$ которое он называл числом Бейса-Хадсона.

Yadryara в сообщении #1690166 писал(а):

Где сумма по нулям большая и положительная

И вот я глянул какая там сумма по дзета-нулям. Миллион нулей-то у меня есть.

Действительно с заданной точностью максимальная положительная сумма именно в этой точке. Покажу фрагмент вычислений:

   1.39818  E316
   1.607    E155

   1.39819  E316
   1.610    E155

   1.39820  E316
   1.633    E155

   1.39821  E316
   1.648    E155

   1.39822  E316
   1.655    E155

   1.39823  E316
   1.650    E155

   1.39824  E316
   1.635    E155

   1.39825  E316
   1.609    E155

   1.39826  E316
   1.616    E155

В первой строчке — $x$, во второй — сумма по миллиону дзета-нулей 2*real(eint1(-log(x)*(1/2+z[i]*I))). Где z[i] и есть $i$-тый ноль, а $i$ пробегает все значения от 1-го до миллиона.

В другом сравнении видно, что нули здесь вошли в резонанс:

    1.00000  E316
    2.959    E153

    1.10000  E316
   10.509    E153

    1.20000  E316
   -1.335    E153

    1.30000  E316
  -81.373    E153

    1.39822  E316
  165.543    E153

В точке 1.39822 сумма по дзета-нулям по модулю в 124 раза больше чем в точке 1.20000.

Кстати, про резонанс говорил и знаменитый Юрий Матиясевич в этой работе: https://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=mp&paperid=263&option_lang=rus

Ю. В. Матиясевич, “Алан Тьюринг и теория чисел”, Матем. просв., сер. 3, 17, Изд-во МЦНМО, М., 2013, 6–34

[vicvolf]

Yadryara в сообщении #1690207 писал(а):

Что это значит? От всех простых? Как именно учитывает?

Я же пояснил.

vicvolf в сообщении #1690175 писал(а):

В данном случае я взял простые до $10^8$. Можно взять больше. Все зависит от требуемой точности.

[Yadryara]

vicvolf, а Вы наоборот возьмите предел поменьше и покажите как посчитали.

[vicvolf]

Простые кортежи с большой длиной и диаметром встречаются довольно редко и первое их появление происходит при больших $x$. Предположим, что выполняется гипотеза Х-Л, тогда количество простых кортежей имеет распределение Пуассона с параметром $a(x)=C_H * x / (\ln x)^k)$. Нам нужно найти вероятность того, что в интервале до $x$ появится хотя бы один такой кортеж.

Поскольку распределение Пуассона, то вероятность, что нет кортежей до $x$:
$P(x)= e^{-a(x)}$.

Вероятность, что есть хотя бы один кортеж до $x$:
$F(x)=1- P(x) = 1 - e^{-a(x)}$.

Тогда вероятность появления первого кортежа до $x$ равна:

$F(x) = 1 - exp(-C_H * x / (\ln x)^k)$

РАСЧЁТ ВЕРОЯТНОСТИ ПЕРВОГО ПОЯВЛЕНИЯ КОРТЕЖА

Используется формула: $F(x) = 1 - exp(-C_H * x / (\ln x)^k)$

Кортеж $H$: 0 2 6 8 12 18 20 26

Константа Харди-Литтлвуда $C_H = 178.26229269$
Длина кортежа $k = 8$

======================================================================
$x$ $C_H*x/(\ln x)^k$ $F(x)$
======================================================================
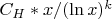
1.00e+02 0.088124 0.08435264
1.50e+02 0.067299 0.06508435
2.25e+02 0.054169 0.05272770
3.38e+02 0.045605 0.04458097
5.06e+02 0.039919 0.03913246
7.59e+02 0.036149 0.03550372
1.14e+03 0.033731 0.03316868
1.71e+03 0.032323 0.03180646
2.56e+03 0.031719 0.03122149
3.84e+03 0.031799 0.03129885
5.77e+03 0.032501 0.03197880
8.65e+03 0.033807 0.03324227
1.30e+04 0.035734 0.03510287
1.95e+04 0.038328 0.03760319
2.92e+04 0.041670 0.04081377
4.38e+04 0.045871 0.04483442
6.57e+04 0.051080 0.04979715
9.85e+04 0.057492 0.05587078
1.48e+05 0.065357 0.06326706
2.22e+05 0.074991 0.07224817
3.33e+05 0.086796 0.08313556
4.99e+05 0.101280 0.09631964
7.48e+05 0.119087 0.11226973
1.12e+06 0.141037 0.13154284
1.68e+06 0.168169 0.15478875
2.53e+06 0.201808 0.18274778
3.79e+06 0.243646 0.21623479
5.68e+06 0.295850 0.25610063
8.52e+06 0.361198 0.30315879
1.28e+07 0.443264 0.35806249
1.92e+07 0.546656 0.42111782
2.88e+07 0.677326 0.49202653
4.31e+07 0.842982 0.56957484
6.47e+07 1.053628 0.65132951
9.71e+07 1.322277 0.73347239
1.46e+08 1.665893 0.81097819
2.18e+08 2.106632 0.87835299
3.28e+08 2.673497 0.93098952
4.91e+08 3.404527 0.96677747
7.37e+08 4.349710 0.98708945
1.11e+09 5.574863 0.99620801
1.66e+09 7.166805 0.99922822

Обратите внимание на строчку: 6.47e+07 1.053628 0.65132951
Это означает, что вероятность появления кортежа при $x=6.47e+07$ равна $0.65132951$.