в чем причина держать в ансамбля одинаковые волновые функции?
В принципе, причина та же, по которой мы в протокол измерений напряжения вольтметром запишем 100 раз одно и то же напряжение, если вольтметр его показывает в 100 актах измерения. Попробуйте сначала детально разобрать совсем тривиальный пример - когда флуктуаций измеряемой величины вообще нет. В примере с вольтметром в этом случае

штук измерений дают одно и то же число

т.е.

В этом случае среднее арифметическое

На языке "статистического ансамбля" это выглядит так: N штук вольтметров разом показывают точно один и тот же результат

без разброса.
В квантовой механике аналогичный тривиальный пример - система, находящаяся в чистом квантовом состоянии, притом в стационарном. Для конкретности примера пусть речь идёт об атоме в основном (т.е. самом нижнем по энергии) состоянии; его волновая функция (в координатном представлении,

- совокупность нужных для такого описания координатных переменных) есть

Пусть

- оператор какой-то физ. величины в атоме, действующий на функции, зависящие от

Тогда квантово-механическое среднее:

Это матричный элемент

с номерами

Тогда то же самое в терминах статистического ансамбля (не просто квантово-механического, а в смысле статистической механики) описывается так: воображаем себе, будто бы на

экземплярах атома проводились такие же квантово-механические измерения (каждое из которых и само по себе не однократный акт, а, как полагается в квантовой механике, включает накопление статистики), и в каждом измерении атомы этого ансамбля обнаруживались в состоянии

без разброса. Т.е. все волновые функции в этом ансамбле получились одинаковые:

Найдём в этом примерчике матрицу плотности согласно Вашему книжному определению. Для этого сначала разложим

по стационарным состояниям:

Тогда:
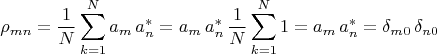
Среднее

в этом простейшем примере микроканонического ансамбля, определяемое через матрицу плотности, совпадает с обычным квантово-механическим:

Аналогично можно поразмыслить над слегка иным примером. Пусть теперь атом слабенько взаимодействует с окружающим его термостатом. Из-за этого взаимодействия атом уже не описывается всё время определённой волновой функцией. В большинстве измерений он проявляет себя по-прежнему как находящийся в основном состоянии

Но иногда (но тоже не в одном, а во многих актах измерения) он ведёт себя как в первом возбуждённом состоянии - с волновой функцией

(Для простоты не учитываю в этом рассуждении кратность вырождения возбуждённого состояния атома.) Ну а состояния с ещё большей энергией

допустим, возбуждаются настолько редко, что такими событиями можно вообще пренебречь.
В таком примере можно приближённо считать, что в

измерениях проявляются только два различных результата. В терминах ансамбля это означает, что среди

волновых функций

много раз встречается

и во много раз меньшее количество раз встречается

а остальных

в таком ансамбле практически нет. Это похоже на канонический ансамбль при очень низкой (по сравнению с энергией возбуждения

температуре.



