Эквивалентные формулировки аксиомы полноты

[bb420]

В статье на Википедии "Непрерывность множества действительных чисел" есть следующее утверждение: "принцип вложенных отрезков сам по себе не равносилен принципу непрерывности Дедекинда. Из принципа непрерывности Дедекинда следует принцип вложенных отрезков, однако для обратного требуется дополнительно потребовать, чтобы упорядоченное поле
R удовлетворяло аксиоме Архимеда". То есть можно найти множество, удовлетворяющее всем аксиомам действительных чисел, кроме аксиомы полноты, не удовлетворяющее принципу Архимеда и удовлетворяющее принципу коши-кантора. Я это множество искал, но не нашёл .Помогите, пожалуйста

[Padawan]

Поле формальных рядов Лорана $\mathbb R ((x))$, вроде бы подходит. $f(x)=\frac{a_{-n}}{x^n}+\frac{a_{-n+1}}{x^{-n+1}}+\ldots+\frac{a_{-1}}x+a_0+a_1x+a_2x^2+\ldots>0$, если первый ненулевой коэффициент (т.е. коэффициет с наименьшим номером) положителен.

Или можно взять поле рациональных функций $\mathbb R(x)$. $f(x)>0$, если существует $a\in\mathbb R$ такое, что $f(x)>0$ для всех $x>a$.

Хотя поле рац. функций может не подойдет.

Сформулируйте четко, пожалуйста, принцип полноты, который Вы хотите, чтобы удовлетворялся.

[dgwuqtj]

Padawan в сообщении #1687793 писал(а):

Поле формальных рядов Лорана $\mathbb R ((x))$, вроде бы подходит.

Можно даже взять $\mathbb Q((x))$. Вообще любое упорядоченное поле имеет пополнение по Коши, но если это поле не удовлетворяло аксиоме Архимеда, то и пополнение ей не будет удовлетворять.

[bb420]

Padawan, вы, наверное, хотели, чтобы я сформулировал чётко принцип полноты, которого я хочу добиться НЕ выполнения. Аксиому полноты я имел в виду как существование супремума у любого подмножества R. Насчёт формальных рядов Лорана и рациональных функций, я их уже рассматривал, но принцип коши кантора там не выполняется, к примеру для лорана

$$ [1; x^{-1}], [2; 0,5*x^{-1}]... $$

не имеют пересечение. Для множества рациональных функций есть похожий пример

[dgwuqtj]

bb420
Есть три разных утверждения про упорядоченное поле $F$:
1) Любая последовательность вложенных отрезков $[a_1, b_1] \supseteq [a_2, b_2] \supseteq [a_3, b_3] \supseteq \ldots$ имеет непустое пересечение.
2) Любая последовательность вложенных отрезков, для которой выполняется $\forall n \in \mathbb N \enskip \exists i \enskip b_i - a_i < \frac 1 n$, имеет непустое пересечение.
3) Любая последовательность вложенных отрезков, для которой выполняется $\forall 0 < \varepsilon \in F \enskip \exists i \enskip b_i - a_i < \varepsilon $, имеет непустое пересечение.
Утверждения (1) и (2) равносильны. Для полей формальных степенных рядов выполнено (3), но не (2), как показывает ваш пример после домножения отрезков на $x$.

Возьмём поле рядов Хана

$$\mathbb R[[x^\Gamma]] = \bigl\{ \sum_{\gamma \in A} a_\gamma x^\gamma \mid a_\gamma \in \mathbb R, A \subseteq \Gamma \text{ вполне упорядоченное} \bigr\},$$

где $\Gamma$ является линейно упорядоченной абелевой группой, в которой $\forall \gamma_1 \leq \gamma_2 \leq \ldots < \ldots \leq \gamma'_2 \leq \gamma'_1 \enskip \exists \gamma \enskip \gamma_1 \leq \gamma_2 \leq \ldots < \gamma < \ldots \leq \gamma'_2 \leq \gamma'_1$. Далее, выделим поле $F \subseteq \mathbb R[[x^\Gamma]]$ из рядов, у которых не более чем счётный носитель (т.е. множество $A$), оно действительно является подполем в силу явных конструкций арифметических операций.

Проверим, что $F$ удовлетворяет (1), т.е. любая последовательность отрезков $[f_1, g_1] \supseteq [f_2, g_2] \supseteq \ldots$ имеет общий элемент $h$, где $f_k = \sum_\gamma f_{k \gamma} x^\gamma$ и $g_k = \sum_t g_{k \gamma} x^\gamma$. Посмотрим на последовательность $\gamma_k$ показателей $g_k - f_k$, т.е. наименьших показателей, при которых коэффициент в $g_k - f_k$ ненулевой. Эта последовательность нестрого возрастает. Рассмотрим два случая.
1) Если эта последовательность стабилизируется, т.е. $\gamma_k = \gamma_{k + 1} = \ldots$, то возьмём в качестве $h$ общий префикс рядов $f_k$ и $g_k$ до показателя $\gamma_k$ и добавим член $h_{\gamma_k} x^{\gamma_k}$, где $h_{\gamma_k}$ лежит в пересечении отрезков $[f_{k \gamma_k}, g_{k \gamma_k}] \supseteq [f_{k + 1, \gamma_k}, g_{k + 1, \gamma_k}] \supseteq \ldots$. Если длины этих отрезков не стремятся к $0$, то выберем $h_{\gamma_k}$ так, чтобы оно было отделено от всех их концов. Иначе, если сами эти отрезки стабилизируются с одной стороны, добавим ещё член $\pm x^{\gamma}$, где $\gamma > \gamma_k$ меньше всех остальных показателей, встречающихся в носителях $f_n$ и $g_n$ после $\gamma_k$.
2) Иначе можно перейти к строго возрастающей подпоследовательности, т.е. не умаляя общности $\gamma_1 < \gamma_2 < \ldots$. В качестве коэффициента $h$ при $x^\gamma$, $\exists k \enskip \gamma < \gamma_k$, возьмём покомпонентный предел $f_{k \gamma}$ (которая стабилизируется там же, где и $g_{k \gamma}$). Если $\gamma_k$ ограничена, то добавим ещё слагаемое $\pm x^\gamma$, где $\gamma$ больше всех $\gamma_k$, но меньше всех показателей из $f_n$ и $g_n$, которые больше всех $\gamma_k$.

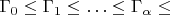
Остаётся предъявить группу $\Gamma$ с требуемым свойством. Построим цепочку упорядоченных векторных пространств $\Gamma_0 \leq \Gamma_1 \leq \ldots \leq \Gamma_\alpha \leq \ldos$ над $\mathbb R$, пронумерованных ординалами, начиная с $\Gamma_0 = \mathbb R$. Если $\alpha$ предельный, то возьмём $\Gamma_\alpha = \bigcup_{\beta < \alpha} \Gamma_\beta$. Иначе пусть $\alpha = \beta + 1$. Если $\Gamma_\beta$ уже имеет требуемое свойство, то мы нашли $\Gamma = \Gamma_\beta$. 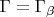В противном случае возьмём наименьший $\gamma < \alpha$, для которого в $\Gamma_\gamma$ найдутся две последовательности из формулировки свойства, которые не имеют строго разделения в $\Gamma_\beta$. Выберем разбиение $\Gamma_\beta = X \sqcup Y$, где $X \leq Y$, $X$ содержит меньшую последовательность, а $Y$ — большую. Положим $\Gamma_\alpha = \Gamma_\beta \oplus \mathbb R x$, где $x \geq g$ тогда и только тогда, когда $g \in X$. По построению, пока $\alpha$ не более чем континуальный, $\Gamma_\alpha$ тоже не более чем континуальное, а если $\kappa$ — первый более чем континуальный ординал (т.е. кардинал $\mathfrak c^{+}$), то $\Gamma_\kappa$ обладает нужным свойством.

-- 28.05.2025, 15:44 --

Можно даже без рядов, только ещё менее конструктивно. Построим цепочку вещественно замкнутых полей $F_0 \subseteq F_1 \subseteq \ldots \subseteq F_\alpha \subseteq \ldots$, пронумерованную ординалами, начиная с какого-то вещественного замыкания $\mathbb R(x)$ для бесконечно малого $x$. Если $\alpha$ предельный, то $F_\alpha = \bigcup_{\beta < \alpha} F_\beta$. Иначе пусть $\alpha = \beta + 1$ и $\gamma < \alpha$ — наименьший ординал, для которого в $F_\gamma$ найдётся последовательность отрезков $[a_1, b_1] \supseteq [a_2, b_2] \supseteq \ldots$ с пустым пересечением в $F_\beta$. Выберем разбиение $F_\beta = X \sqcup Y$, где $X \leq Y$, и в качестве $F_\alpha$ возьмём некоторое вещественное замыкание $F_\beta(x)$, где $P(x) > 0$ тогда и только тогда, когда рациональная функция $P$ принимает положительные значения во всех достаточно больших элементах $X$ и достаточно малых элементах $Y$ (здесь для корректности важно, что поле вещественно замкнуто). Пока $\alpha$ не более чем континуальный, поле $F_\alpha$ тоже не более чем континуальное, а следующее за ними всеми поле $F_{\mathfrak c^{+}}$ обладает свойством (1).

[wrest]

bb420 в сообщении #1687790 писал(а):

Помогите, пожалуйста

Множество гипервещественных чисел