bb420Есть три разных утверждения про упорядоченное поле

:
1) Любая последовательность вложенных отрезков
![$[a_1, b_1] \supseteq [a_2, b_2] \supseteq [a_3, b_3] \supseteq \ldots$ $[a_1, b_1] \supseteq [a_2, b_2] \supseteq [a_3, b_3] \supseteq \ldots$](https://dxdy-02.korotkov.co.uk/f/1/b/6/1b681538908f34f357393f7ba308502882.png)
имеет непустое пересечение.
2) Любая последовательность вложенных отрезков, для которой выполняется

, имеет непустое пересечение.
3) Любая последовательность вложенных отрезков, для которой выполняется

, имеет непустое пересечение.
Утверждения (1) и (2) равносильны. Для полей формальных степенных рядов выполнено (3), но не (2), как показывает ваш пример после домножения отрезков на

.
Возьмём
поле рядов Хана![$$\mathbb R[[x^\Gamma]] = \bigl\{ \sum_{\gamma \in A} a_\gamma x^\gamma \mid a_\gamma \in \mathbb R, A \subseteq \Gamma \text{ вполне упорядоченное} \bigr\},$$ $$\mathbb R[[x^\Gamma]] = \bigl\{ \sum_{\gamma \in A} a_\gamma x^\gamma \mid a_\gamma \in \mathbb R, A \subseteq \Gamma \text{ вполне упорядоченное} \bigr\},$$](https://dxdy-02.korotkov.co.uk/f/5/3/5/535ccfbf410fb226098f329e7821969182.png)
где

является линейно упорядоченной абелевой группой, в которой

. Далее, выделим поле
![$F \subseteq \mathbb R[[x^\Gamma]]$ $F \subseteq \mathbb R[[x^\Gamma]]$](https://dxdy-04.korotkov.co.uk/f/f/a/4/fa483e10b33cc610236e88b08253439582.png)
из рядов, у которых не более чем счётный носитель (т.е. множество

), оно действительно является подполем в силу явных конструкций арифметических операций.
Проверим, что

удовлетворяет (1), т.е. любая последовательность отрезков
![$[f_1, g_1] \supseteq [f_2, g_2] \supseteq \ldots$ $[f_1, g_1] \supseteq [f_2, g_2] \supseteq \ldots$](https://dxdy-01.korotkov.co.uk/f/8/0/c/80c0e435eaafc80e6c8cdd591568110782.png)
имеет общий элемент
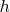
, где

и

. Посмотрим на последовательность

показателей

, т.е. наименьших показателей, при которых коэффициент в

ненулевой. Эта последовательность нестрого возрастает. Рассмотрим два случая.
1) Если эта последовательность стабилизируется, т.е.

, то возьмём в качестве
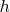
общий префикс рядов

и

до показателя

и добавим член

, где

лежит в пересечении отрезков
![$[f_{k \gamma_k}, g_{k \gamma_k}] \supseteq [f_{k + 1, \gamma_k}, g_{k + 1, \gamma_k}] \supseteq \ldots$ $[f_{k \gamma_k}, g_{k \gamma_k}] \supseteq [f_{k + 1, \gamma_k}, g_{k + 1, \gamma_k}] \supseteq \ldots$](https://dxdy-04.korotkov.co.uk/f/7/e/2/7e282cd0be3f0f0b04d2e7fd385b0f9c82.png)
. Если длины этих отрезков не стремятся к

, то выберем

так, чтобы оно было отделено от всех их концов. Иначе, если сами эти отрезки стабилизируются с одной стороны, добавим ещё член

, где

меньше всех остальных показателей, встречающихся в носителях
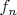
и

после

.
2) Иначе можно перейти к строго возрастающей подпоследовательности, т.е. не умаляя общности

. В качестве коэффициента
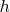
при

,

, возьмём покомпонентный предел

(которая стабилизируется там же, где и

). Если

ограничена, то добавим ещё слагаемое

, где

больше всех

, но меньше всех показателей из
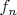
и

, которые больше всех

.
Остаётся предъявить группу

с требуемым свойством. Построим цепочку упорядоченных векторных пространств
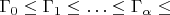
над
, пронумерованных ординалами, начиная с

. Если

предельный, то возьмём

. Иначе пусть

. Если

уже имеет требуемое свойство, то мы нашли
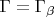
. В противном случае возьмём наименьший

, для которого в

найдутся две последовательности из формулировки свойства, которые не имеют строго разделения в

. Выберем разбиение

, где

,

содержит меньшую последовательность, а

— большую. Положим

, где

тогда и только тогда, когда

. По построению, пока

не более чем континуальный,

тоже не более чем континуальное, а если

— первый более чем континуальный ординал (т.е. кардинал

), то

обладает нужным свойством.
-- 28.05.2025, 15:44 --Можно даже без рядов, только ещё менее конструктивно. Построим цепочку вещественно замкнутых полей

, пронумерованную ординалами, начиная с какого-то вещественного замыкания

для бесконечно малого

. Если

предельный, то

. Иначе пусть

и

— наименьший ординал, для которого в

найдётся последовательность отрезков
![$[a_1, b_1] \supseteq [a_2, b_2] \supseteq \ldots$ $[a_1, b_1] \supseteq [a_2, b_2] \supseteq \ldots$](https://dxdy-04.korotkov.co.uk/f/7/6/7/767a0aa8d85e41b55c61fe0acedf577982.png)
с пустым пересечением в

. Выберем разбиение

, где

, и в качестве

возьмём некоторое вещественное замыкание

, где

тогда и только тогда, когда рациональная функция

принимает положительные значения во всех достаточно больших элементах

и достаточно малых элементах

(здесь для корректности важно, что поле вещественно замкнуто). Пока

не более чем континуальный, поле

тоже не более чем континуальное, а следующее за ними всеми поле

обладает свойством (1).