Тогда так.
Пусть

— ограниченная квази-восходящая последовательность. Пусть она расходится. Тогда она должна содержать как минимум две подпоследовательности, сходящихся к разным пределам. Предположим, что

и

- такие две подпоследовательности. Пусть также

.
Для любого

, существует

такое, что для любых

будет

и

.
Так как

- квази-восходящая, то для любого

существует

такое, что если

, то

.
Положим

и

, тогда оба условия выше должны выполняться. Пусть

. Тогда
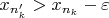
.
Из определения предела

. Подставляя в предыдущее неравенство, получим

.
Из выражения для

имеем

. Подставляя в предыдущее неравенство, получаем

.
Следовательно,
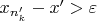
, что противоречит тому, что

- это предел для

.



