### **Формальный анализ плотности метрики при частотном смешении**
#### **1. Исходное пространство сигналов**
Пусть имеется гильбертово пространство сигналов
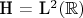
) с базисом из эрмитовых функций:
![[\
\psi_n(t) = \frac{1}{\sqrt{2^n n! \sqrt{\pi}}} H_n(t) e^{-t^2/2}, \quad n = 0, 1, 2, \dots
\] [\
\psi_n(t) = \frac{1}{\sqrt{2^n n! \sqrt{\pi}}} H_n(t) e^{-t^2/2}, \quad n = 0, 1, 2, \dots
\]](https://dxdy-01.korotkov.co.uk/f/c/b/5/cb5c016da113786b2b908131a43ad90a82.png)
- **Метрика** между двумя сигналами

:
![\[
d(f, g) = \|f - g\| = \sqrt{\int_{-\infty}^\infty |f(t) - g(t)|^2 dt}.
\] \[
d(f, g) = \|f - g\| = \sqrt{\int_{-\infty}^\infty |f(t) - g(t)|^2 dt}.
\]](https://dxdy-04.korotkov.co.uk/f/b/9/a/b9ab8b9b5c45c971a8b2e4da17daca7182.png)
- **Плотность метрики** характеризуется числом значимых базисных функций, требуемых для аппроксимации сигналов.
---
#### **2. Частотное смешение и расширение пространства**
При смешении двух сигналов

и

их произведение
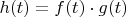
требует большего числа базисных функций для представления.
##### **Разложение по эрмитовым функциям**
Если:
![\[
f(t) = \sum_{k=0}^N a_k \psi_k(t), \quad g(t) = \sum_{m=0}^M b_m \psi_m(t),
\] \[
f(t) = \sum_{k=0}^N a_k \psi_k(t), \quad g(t) = \sum_{m=0}^M b_m \psi_m(t),
\]](https://dxdy-03.korotkov.co.uk/f/2/2/1/2211c9672d0ff4f48b87e55fe3fcdc3e82.png)
то их произведение:
![\[
h(t) = \sum_{k=0}^N \sum_{m=0}^M a_k b_m \psi_k(t) \psi_m(t).
\] \[
h(t) = \sum_{k=0}^N \sum_{m=0}^M a_k b_m \psi_k(t) \psi_m(t).
\]](https://dxdy-02.korotkov.co.uk/f/5/c/a/5ca885d5884dff124cbcd4606adc921582.png)
Используя формулу произведения эрмитовых функций:
![\[
\psi_k(t) \psi_m(t) = \sum_{s=0}^{\min(k,m)} c_s^{k,m} \psi_{k+m-2s}(t),
\] \[
\psi_k(t) \psi_m(t) = \sum_{s=0}^{\min(k,m)} c_s^{k,m} \psi_{k+m-2s}(t),
\]](https://dxdy-03.korotkov.co.uk/f/e/3/d/e3d02eaf2e0b8ca11303f59c97afd5b982.png)
где коэффициенты

определяются ортогональностью. Таким образом,

лежит в подпространстве размерности

.
---
#### **3. Изменение плотности метрики**
- **Исходная плотность**:
Число базисных функций

.
- **После смешения**:
Число базисных функций

.
### **Выводы**
1. **Рост размерности**:
Смешение сигналов расширяет пространство представления, увеличивая число базисных функций.
2. **Изменение метрики**:
Расстояния между сигналами измеряются в более "густом" пространстве, что делает метрику более чувствительной.
3. **Физическая интерпретация**:
Появление новых частотных компонент эквивалентно добавлению новых осей в пространстве состояний, увеличивая его ёмкость.
Формально это описывается тензорным произведением пространств и ростом энтропии сигнала. Для строгих приложений (например, квантовая механика или сжатие данных) требуется учет спектральных плотностей.
-- 12.05.2025, 21:56 --Подскажите, можно ли доверять этой информации?
-- 12.05.2025, 21:58 --Это ответ DeepSeek
-- 12.05.2025, 22:10 --Можно ли сказать, что затухание будет происходить по причине роста плотности метрики?
-- 12.05.2025, 22:13 --При частотном смешении



