Тессеракт (4-х мерный куб)

[StepV]

Помогите разобраться, правильно ли я понимаю. Если современному человеку попадется (совершенно случайно ) в руки тессеракт, выглядящий в нашем пространстве, как трехмерный куб, то исследователь никаким способом не сможет определить, что это четырехмерная фигура, т.к. задать направление вращения или движения в направлении четвертой координаты он не сможет.
Единственный возможный вариант - это удар с разрушением, в этом случае получатся осколки, которые не удастся сложить в первоначальный трехмерный куб.

[dgwuqtj]

StepV в сообщении #1684951 писал(а):

Если современному человеку попадется (совершенно случайно ) в руки тессеракт,

То придётся переписывать всю физику и вопросы о вращениях/движениях отложат на неопределённый срок. Хотя бы пока с терминологией не определятся.

[StepV]

Вопрос чисто математический. На изменения в физике не претендующий. Известно, если 4-мерный куб вращать в 4-x мерном пространстве, то в трехмерном подпространстве его форма будет искажаться. Если же вращения будут задаваться в трехмерном подпространстве, то у нас все время получается трехмерный куб без всяких искажений. Т.е. мы не сможем различить тессеракт и куб на основе операций в трехмерном подпространстве.
Выводы сделаны из следующих соображений:
$e_1=(1,0,0,0)$; $e_2=(0,1,0,0)$; $e_3=(0,0,1,0)$; $e_4=(0,0,0,1)$
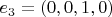
Начало векторов и их вершины образуют единичный четырехмерный куб, а вектора $e_1,e_2,e_3$ образуют трехмерный куб. Если использовать для преобразования векторов некоторую матрицу поворота $A$, в которой $a_{44}=1$, а остальные элементы по четвертой горизонтали и вертикали нули, то у нас поворот производится в трехмерном пространстве. При чем новые получившиеся вектора $u_1,u_2,u_3$ будут перпендикулярны между собой и перпендикулярны $e_4$, в трехмерном пространстве мы получим опять трехмерный куб, но повернутый. Получается, что в трехмерном подпространстве мы не сможем отличить 4-х мерный куб от трехмерного.
Действительно это так или я где-то ошибаюсь?

[dgwuqtj]

StepV в сообщении #1684999 писал(а):

Известно, если 4-мерный куб вращать в 4-x мерном пространстве, то в трехмерном подпространстве его форма будет искажаться. Если же вращения будут задаваться в трехмерном подпространстве, то у нас все время получается трехмерный куб без всяких искажений.

Давайте тогда определение "формы тессеракта в трёхмерном подпространстве". Это сечение, ортогональная проекция, или что-то ещё?

[StepV]

dgwuqtj в сообщении #1685010 писал(а):

Это сечение, ортогональная проекция, или что-то ещё?

Пусть ребро тессеракта равно $a$, оси определяем буквами: $x,y,z,w$. Тессеракт начинается от начала системы координат. Тогда мы имеем трехмерное сечение тессеракта, к которому принадлежат точки с координатами:
$0 \leqslant x \leqslant a$; $0 \leqslant y \leqslant a$; $0 \leqslant z \leqslant a$ и с постоянной координатой $w$, равной, например, $w=\frac a n$, где $ n > 0$.

[dgwuqtj]

Окей. А если вращать, то что, будем пересекать повёрнутый гиперкуб этой же гиперплоскостью $w = \frac a n$? Легко так повернуть гиперкуб вокруг начала координат, что сечение станет пустым.

[Dmitriy40]

По моему если вращать (или двигать) многомерный объект в подпространстве (т.е. вокруг любой оси, перпендикулярной подпространству), то его сечение в этом подпространстве никак не изменится (только повернётся или сдвинется). Речь же не идёт про вращение во внешнем пространстве. Соответственно ответ на исходный вопрос - нет, никак не отличить. Если только математически. А физически - легко, хоть бы по плотности, не одноатомный же он во всех дополнительных измерениях.

[StepV]

dgwuqtj в сообщении #1685027 писал(а):

Легко так повернуть гиперкуб вокруг начала координат, что сечение станет пустым.

Для иллюстрации моей мысли давайте скатимся на одно измерение меньше. Пусть трехмерный куб пересечен плоскостью так, что в сечении получается квадрат. Теперь, как мы не пытаемся вращать и сдвигать квадрат в этой плоскости, результатом будет все тот же квадрат, но повернутый на угол. Так и в примере с тессерактом все вращения являются трехмерными внутри гиперплоскости $ w = \frac a n$

[dgwuqtj]

Тогда всё верно, конечно.

[Dmitriy40]

Только тессеракт может попасть в руки и не как трёхмерный куб (как и сечение куба не обязательно квадрат) ... Но это ничего не изменит - математическими операциями (поворот, сдвиг) в трехмерном пространстве его многомерность не установить.

[StepV]

Dmitriy40 в сообщении #1685033 писал(а):

Только тессеракт может попасть в руки и не как трёхмерный куб (как и сечение куба не обязательно квадрат) ..

Спасибо, это понятно. Главное, чтобы он попал в руки , а уж тогда и поэксперементируем.

[B@R5uk]

Тут, кстати, интересный вопрос возникает в связи с сечениями. Сечение куба плоскостью может представлять из себя фигуры от треугольника до шестиугольника. Причём правильный шестиугольник (проходящий через центр куба, перпендикулярный одной из его диагоналей и имеющий вершины в центрах трёх пар противоположных рёбер), если я не ошибаюсь, является сечением максимальной площади. Какова, интересно, номенклатура трёхмерных тел, которые являются сечениями тессеракта трёхмерной гиперплоскостью, и которое из них имеет максимальный объём?

[drzewo]

Я бы поставил на то, что это давно известно.