Количество теплоты, поглощенное газом.

[realeugene]

Моль - он так же безразмерен, как радиан. Но моли всё-таки обычно пишут в единицах измерения.

[sergey zhukov]

Cos(x-pi/2)
А что в молях тогда измеряется? Есть же такая единица измерения? Она даже одна из основных в СИ.

Я лично считаю, что в уравнении Менделеева-Клапейрона, которое мы тут используем, стоит размерная величина $\nu$ - количество вещества, которое измеряется в молях. И размерности я всегда с учетом молей проверяю. Еще никогда никаких проблем с этим не возникало.

[realeugene]

sergey zhukov в сообщении #1683730 писал(а):

Я лично считаю, что в уравнении Менделеева-Клапейрона, которое мы тут используем, стоит размерная величина $\nu$ - количество вещества, которое измеряется в молях.

Если строго, то целые числа и их масштабированные величины безразмерны. Количество молекул - целое число по определению.

[EUgeneUS]

Возникает забавный вопрос: а величина в "штуках" - это размерная или безразмерная величина?

[sergey zhukov]

realeugene в сообщении #1683731 писал(а):

целые числа и их масштабированные величины безразмерны

Это потому, что кажется естественным за единицу принять минимальное значение дискретной величины. Не нужно выдумывать произвольный эталон, он создан самой дискретной природой измеряемой величины. Но с какой стати это обязательно так принимать? Я могу за единицу принять любое количество "квантов" (и даже нецелое их число, если захочу). Вот как с молем.

[realeugene]

sergey zhukov в сообщении #1683734 писал(а):

Это потому, что кажется естественным за единицу принять минимальное значение дискретной величины.

Нет, это потому, что все размерные физические величины непрерывны и осмысленны только как отношение к некоторому своему эталону, это отношение - действительное число. А штуки - просто штуки, они дискретны, описываются натуральными числами и в эталоне штуки не нуждаются.

[sergey zhukov]

Кулон, кстати, тоже безразмерная величина. Ее нужно в штуках считать.

[realeugene]

sergey zhukov в сообщении #1683738 писал(а):

Кулон, кстати, тоже безразмерная величина. Ее нужно в штуках считать.

Уже да.

Кстати, при оценке дробового шума проще пересчитать в количество электронов и извлечь из него квадратный корень.

[Cos(x-pi/2)]

(Оффтоп)

Топикстартер решает задачу из конкретной книги, и там все определения, которые ему нужны, написаны. Предположение об опечатке в ответе здесь уже высказано. Поэтому развивать длинный оффтоп про что такое моль, штуки и т.п. нежелательно.

Подчеркну только, что СИ - не самая удачная система для осмысления законов физики; на ней сказалась витиеватая история открытий. Уравнение состояния идеального газа в его итоговом понимании выглядит просто:

$$pV=NkT$$

где $N$ - число молекул газа в объёме $V.$ Здесь $pV$ имеет размерность энергии, и $kT$ имеет размерность энергии. Поэтому $N$ - с очевидностью безразмерное число. Ни о каких молях в этом уравнении речи нет.

Моль это мера для введённого в XIX веке понятия "количество вещества", когда люди ещё не знали свойств молекул, не умели молекулы подсчитывать, не знали постоянной Больцмана $k,$ и много чего ещё не знали. Теперь же мы знаем, что "1 моль газа" это $N_A$ штук молекул; столько их содержится в $12$ граммах изотопа углерода ${}^{12}\text{С},$ по определению числа $N_A.$ Поэтому для придания уравнению состояния идеального газа его исторического внешнего вида, можно величину $NkT$ записать так:

$$NkT=\dfrac{N}{N_A}N_A\,kT=\nu RT$$

где по определению $\nu=N/N_A$ есть безразмерное число, $R=N_Ak$ есть постоянная с размерностью $\text{энергия}/\text{абс.температура},$ как у постоянной Больцмана. (В книге бытия нумер пять § 42 так и написано: $R=8.314\cdot 10^7$ эрг/град. Это в системе СГС.)

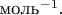
В СИ условились величине $\nu$ приписывать единицу измерения $\text{моль}$ (вероятно для большего историзма и просто для напоминания того факта, что $\nu$ это количество молей газа, вычисляемое как $N/N_A).$ Тогда в единице измерения для $R$ приходится дописывать множитель $\text{моль}^{-1}.$ Ну и число $N_A$ тогда надо считать не безразмерным, а имеющим единицу измерения $\text{моль}^{-1}.$

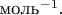
Т.е. эта морока с молями в единицах измерения для величин в уравнении состояния идеального газа - отголосок тех времён, когда учёные почувствовали, что им требуется понятие "одинаковые количества вещества" для разных веществ, но искомое понятие не совпадает с понятием "одинаковые массы вещества". А количества молекул подсчитывать ещё не умели, умели находить только отношения масс молекул. Вот и ввели в дело этакий костыль: моль. В практической работе он оказался удобным, так как легко выражается через массу вещества, т.е. через величину, удобную для практических измерений.

Для обдумывания же уравнений физики более удобна система СГС. В частности, уравнение состояния идеального газа проще выглядит без молей: $pV=NkT.$

Кроме того, на мой взгляд, полезно различать понятия "размерность физической величины" и "единица измерения физической величины". Размерности разных величин выражаются через размерности "длины", "массы", "времени" и их комбинации. Например: $\text{скорость}=\text{длина}/\text{время},$ $\text{сила}=\text{масса}\cdot\text{длина}\cdot\text{время}^{-2},$ $\text{энергия}=\text{масса}\cdot\text{скорость}^2=\text{сила}\cdot\text{длина},$ $\text{давление}=\text{сила}\cdot\text{длина}^{-2},$ $\text{объём}=\text{длина}^3.$ Размерность физ. величины нельзя произвольно поменять; это как бы сам физ.смысл данной величины. А единица измерения может быть выбрана произвольно. Например, длину можно измерять в метрах, в ангстремах, в саженях, в аршинах, в локтях, в футах, в дюймах, в милях, и т.д., в любых их долях. В конкретных задачах удобные для решения задачи единицы длины нередко составляются из величин, заданных в задаче, а не берутся из каких-то готовых систем единиц.

Штуки - безразмерные. Например, о длине $L=5\,\text{м}$ можно сказать. что это "пять штук метров"; тогда "пять штук" это безразмерное число, но оно умножается на размерную единицу длины $L_1=1\,\text{м}.$ То есть $L=(5\,\text{шт})\cdot (1\,\text{м})=5\,L_1$ есть величина с размерностью длины, так как $L_1$ имеет размерность длины. Величина $L/L_1$ - безразмерная.

Кулон - не безразмерная величина, это величина с размерностью $\text{заряд}=\text{сила}^{1/2}\cdot \text{длина}.$ Например, если за единицу заряда выбрать абсолютную величину заряда электрона $|q_e|,$ то заряд $q=1\,\text{Кл}$ запишется (здесь и дальше пишу всё приближённо) как $q=0.625\cdot 10^{19}|q_e|.$

Т.е. $0.625\cdot 10^{19}$ штук электронов (это безразмерное число) имеют суммарный заряд (это физическая величина $q$ с размерностью "заряд"), равный $0.625\cdot 10^{19}|q_e|.$ Другими словами, в СИ заряд электрона без учёта его отрицательного знака равен $|q_e|=1.6\cdot 10^{-19}\,\text{Кл}.$

В системе СГС единица заряда $q_{\text{СГС}}=1\,\text{дин}^{1/2}\cdot \text{см}$ такова, что (тоже приближённо) $|q_e|=4.8\cdot 10^{-10} q_{\text{СГС}.$ Видим, что $1\,\text{Кл}=3\cdot 10^9\,q_{\text{СГС}.$ Значит, если нам будет дан заряд $q_{(\text{Кл})},$ измеренный в кулонах, то можно его выразить через величину заряда $q_{(\text{СГС })},$ измеренную в единицах заряда СГС, по формуле $q_{(\text{СГС})}=3\cdot 10^9 q_{(\text{Кл})}. $

В системе СГС закон Кулона для силы взаимодействия двух зарядов в вакууме записывается без каких-либо дополнительных множителей:

$$F_{(\text{дин})}=\dfrac{q_{1(\text{СГС})}\,q_{2(\text{СГС})}} {r_{(\text{см})}^2}\qquad (\text{СГС})$$

В скобках здесь указаны единицы измерения величин, присутствующих в этой формуле.

Если нам даны заряды в единицах СИ, то прежде, чем подставить их в эту формулу, надо перевести их в единицы СГС; имеем приближённо:

$$q_{1(\text{СГС})}\,q_{2(\text{СГС})}=(3\cdot 10^9)^2q_{1(\text{Кл})}\,q_{2(\text{Кл})}$$

Если расстояние дано в метрах, то переводим его в сантиметры:

$$r_{(\text{см})}^2}=10^4 r_{(\text{м})}^2}$$

И если сила дана в ньютонах, то переводим её в дины (одна дина это $1\,\text{г}\cdot \text{см}\cdot \text{c}^{-2}=10^{-5}\,\text{Н}):$

$$F_{(\text{дин})}=10^5F_{(\text{Н})}$$

Подставив всё это в формулу $(\text{СГС}),$ получаем равенство

$$10^5F_{(\text{Н})}=\dfrac{(3\cdot 10^9)^2q_{1(\text{Кл})}\,q_{2(\text{Кл})}}{10^4 r_{(\text{м})}^2}$$

то есть получилась формула закона Кулона в СИ:

$$F_{(\text{Н})}\,=\, k\,\dfrac{q_{1(\text{Кл})}\,q_{2(\text{Кл})}}{r_{(\text{м})}^2}\qquad (\text{СИ})$$

где

$$k\,=\,10^{-5}\,\dfrac{(3\cdot 10^9)^2}{10^4}=9\cdot 10^9$$

Мне при вычислениях и проверках размерностей удобно думать о величинах в этой формуле $(\text{СИ})$ как об имеющих размерности силы, заряда и длины, а коэффициент $k$ считать безразмерным множителем, возникшим от произвола в выборе единиц. Формально же, по правилам СИ, $k$ имеет некую составную единицу измерения, притом все единицы измерения обычно называются "размерностями." Думаю, всё это в конце концов дело привычки.

[EUgeneUS]

Cos(x-pi/2)
В очередной раз позвольте выразить восхищение Вашим подробным и исчерпывающим разбором вопроса.

Но хотел бы обратить внимание вот на что:

Cos(x-pi/2) в сообщении #1683760 писал(а):

Кроме того, на мой взгляд, полезно различать понятия "размерность физической величины" и "единица измерения физической величины".

Действительно так. При этом у безразмерной величины могут быть единицы измерения, и даже разные для одной и той же - со своими переводными коэффициентами (моли - штуки молекул, радианы - угловые градусы). Указание \ учёт этих единиц измерения в анализе размерностей скорее помогает, чем мешает.

По задаче из стартового поста.
Что произойдет, если увеличим систему в $n$ раз (например, имеем $n$ одинаковых систем)?
Изменение теплоты, объем и количество вещества - величины аддитивные. Увеличатся в $n$ раз
Давление и температура - останутся теми же.

Объем входит в ответ линейно. Значит количество вещества не должно войти в ответ в явном виде, иначе изменение теплоты не будет увеличиваться линейно.

[realeugene]

Cos(x-pi/2) в сообщении #1683760 писал(а):

Штуки - безразмерные. Например, о длине $L=5\,\text{м}$ можно сказать. что это "пять штук метров"

Нет, нельзя так сказать. Штуки - целые числа, а длина делится как угодно.

Кроме равенств, размерности полезны, когда выражения стоят как аргументы трансцендентных и иногда просто иррациональных функций. Такие выражения должны быть безразмерными. При этом, логарифмы от штук и синусы от радиан можно вычислять, а от метров - нет.

-- 26.04.2025, 11:10 --

Cos(x-pi/2) в сообщении #1683760 писал(а):

Кулон - не безразмерная величина, это величина с размерностью $\text{заряд}=\text{сила}^{1/2}\cdot \text{длина}.$

Кулон - это величина с размерностью количества штук элементарных зарядов. То, что у вас в размерности стоит квадратный корень из силы уже доказательство того, что или размерность силы не может быть базовой для системы единиц, или вы неправильно записали размерность заряда. Нельзя из базовых размерностей извлекать квадратные корни.

В электродинамике Максвелла заряд бесконечно делим, поэтому, если забыть про квантовые эффекты, заряды можно считать размерными физвеличинами. Но не надо забывать, что диэлектрическая проницаемость - тоже размерная величина, которая в некоторых системах единиц "для удобства" приравнивается к единице для вакуума.

[sergey zhukov]

EUgeneUS в сообщении #1683771 писал(а):

у безразмерной величины могут быть единицы измерения

Звучит странновато. Хотя и правильно. Скажем, проценты.