Добрый день, прошу прощения за беспокойство.
(дисклеймер)
Да, весна, да, весеннее обострение. Очень сильно извиняюсь.
ВведениеДавеча, во время очередного переосмысления периодического закона и правил заполнения электронной оболочки, захотелось записать себе функциональную зависимость правила Хунда от зарядового числа атома
Z, но к сожалению ничего подобного найти не удалось, поэтому заинтересовался, не возможно ли такое где-нибудь?
Для тех, кто забыл, электронное строение атомов в
периодической системе Д.И. Менделеева даётся набором следующих правил.
- Число электронов в атоме даётся зарядовым числом ядра Z. Это порядковый номер элемента в периодической таблице (
 -- это водород,
-- это водород,  -- бериллий, ведь он между бором и литием,
-- бериллий, ведь он между бором и литием,  -- углерод, и т.д.), а по совместительству количество протонов в ядре.
-- углерод, и т.д.), а по совместительству количество протонов в ядре. - Электроны располагаются на орбиталях водородоподобного атома, дающихся тремя квантовыми числами:
 -- главное квантовое число,
-- главное квантовое число,  -- орбитальное квантовое число (форма орбитали,
-- орбитальное квантовое число (форма орбитали,  -- это s-орбитали,
-- это s-орбитали,  -- p-орбитали, и т.д.), и конкретная орбиталь даётся магнитным квантовым числом
-- p-орбитали, и т.д.), и конкретная орбиталь даётся магнитным квантовым числом  (всего орбиталей для числа l имеется
(всего орбиталей для числа l имеется  штука).
штука). - На каждой орбитали может располагаться максимум два электрона, с противоположными спинами (спиновое квантовое число
 для электронов со спином вверх/вниз).
для электронов со спином вверх/вниз). - Спиновые числа для двух электронов совпадать не могут (принцип Паули).
- Орбитали заполняются в порядке возрастания чисел
 , при одинаковых значениях
, при одинаковых значениях  , сначала заполняется
, сначала заполняется  -подуровень с меньшим главным квантовым числом (правило Клечковского или правило Маделунга).
-подуровень с меньшим главным квантовым числом (правило Клечковского или правило Маделунга). - При заполнении подуровня
 , максимизируется суммарный спин на этом подуровне (правило Хунда).
, максимизируется суммарный спин на этом подуровне (правило Хунда).
Этого достаточно, чтобы восстановить структуру электронных оболочек каждого (ну или почти каждого) атома в периодической системе. Но, как можно заметить, что у нас наши правила имеют вид рекурсивного алгоритма, где для установления оболочки следующего элемента, нам нужно знать распределение электронов в атоме предыдущего элемента.
Собственно, отсюда возник вопрос:
А можно ли восстановить ныне заполняемую пару квантовых чисел  и максимально заполненный уровень
и максимально заполненный уровень  (т.е. период элемента) напрямую из зарядового числа Z?
(т.е. период элемента) напрямую из зарядового числа Z?Естественно, здесь правило Хунда не рассматривается за ненадобностью для задачи.
Попытка решенияСобственно, в качестве попытки решения, отталкивался я от квантового числа

, поскольку уровни заполняются монотонно с возрастанием этого квантового числа. При заданном квантовом числе
M, у нас возможны следующие комбинации

:
Отсюда мы можем вычислить, сколько всего электронов вмещается на уровень

:

Далее, мы можем сказать, сколько максимально у нас имеется электронов от уровня

до уровня

, это

Последняя формула была взята с OEIS (последовательность
A168380), и да, это только вторая из последовательностей, перечисленных здесь, которую удалось найти в OEIS. Первая была

, или период элемента как функция от заряда (
A058318), но там нет функциональной зависимости

.
Дальше, можно попробовать найти

, принимая
M непрерывным, и решая получающееся кубическое уравнение. У нас получаются два случая: для чётного и для нечётного
M,
- В случае нечётного M мы приходим к уравнению
 .
. - В случае чётного M мы приходим к уравнению
 .
.
Их мы можем решить при помощи компьютерных систем символических вычислений (чтобы не напортачить).
(код для wxMaxima)
Код:
solve(x^3 + 3*x^2 + 5*x +(3- 6*z)=0,x);
solve(x^3 + 3*x^2 + 2*x - 6*z=0,x);
Единственные действительные корни имеют следующий вид:

для нечётного
M и

для чётного
M. А дальше у меня что-то не идёт...
Какая была идея дальше?Идея была в том, чтобы сшить эти два решения для

, чтобы у нас получалась правильная последовательность целых чисел. Но я совершенно не представляю как это делается, и какие методы для этого существуют (собственно, поэтому и пишу сообщение в данный раздел).
После того, как имелась бы функциональная зависимость (не важно насколько страшная, главное какая-то), её можно было бы использовать, чтобы найти число электронов на
M-м уровне при атомном номере
Z как

А уже из этого числа и числа
M каким-то образом найти ныне заполняемое

(и значит
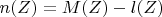
), и

. Но тут я даже не вижу как это можно сделать (тоже наверное какая-то степенная зависимость, но не пойму как её получить).
Зачем этим вообще заниматься?Ну, во-первых, это просто прикольно. Ведь странно, что не получается найти даже очень страшные формулы, которые бы давали искомые зависимости. Ну, а во-вторых, это всё связано с тем самым периодическим законом. Когда мы смотрим на всякие численные зависимости физических величин от зарядового числа, например, потенциалов ионизации атомов:

то мы действительно видим периодичность, но при этом период у нас увеличивается с ростом заряда ядра

, что видно из абсолютно любой версии графического представления периодической системы. И вот, есть надежда, что если есть искомые функциональные зависимости, то можно было бы, например, взять непрерывный аналог этих выражений, и решить, например, уравнение

, откуда получить ещё одно непрерывное выражение для эффективного заряда ядра

, которое бы делала эти все графики по-настоящему периодическими (чтобы можно было сделать преобразование Фурье, вытащить периоды, затухания и прочее).
Спасибо за внимание.P.S.В дополнение к вышесказанному (вдруг кому-то захочется тоже самостоятельно попробовать поиграться с этой задачей), вот численные последовательности всех перечисленных квантовых чисел, которые можно экспортировать в Excel, LibreOffice Calc, в питоновский скрипт, и т.д. и т.п.
(данные)
Первый столбец -- это номер элемента
Z, второй -- период элемента

(взята из
OEIS A058318), третий и четвёртый -- это, соответственно,
n и
l заполняемой орбитали, а пятый -- это

.
Код:
#Z nmax n l M=n+l
1 1 1 0 1
2 1 1 0 1
3 2 2 0 2
4 2 2 0 2
5 2 2 1 3
6 2 2 1 3
7 2 2 1 3
8 2 2 1 3
9 2 2 1 3
10 2 2 1 3
11 3 3 0 3
12 3 3 0 3
13 3 3 1 4
14 3 3 1 4
15 3 3 1 4
16 3 3 1 4
17 3 3 1 4
18 3 3 1 4
19 4 4 0 4
20 4 4 0 4
21 4 3 2 5
22 4 3 2 5
23 4 3 2 5
24 4 3 2 5
25 4 3 2 5
26 4 3 2 5
27 4 3 2 5
28 4 3 2 5
29 4 3 2 5
30 4 3 2 5
31 4 4 1 5
32 4 4 1 5
33 4 4 1 5
34 4 4 1 5
35 4 4 1 5
36 4 4 1 5
37 5 5 0 5
38 5 5 0 5
39 5 4 2 6
40 5 4 2 6
41 5 4 2 6
42 5 4 2 6
43 5 4 2 6
44 5 4 2 6
45 5 4 2 6
46 5 4 2 6
47 5 4 2 6
48 5 4 2 6
49 5 5 1 6
50 5 5 1 6
51 5 5 1 6
52 5 5 1 6
53 5 5 1 6
54 5 5 1 6
55 6 6 0 6
56 6 6 0 6
57 6 4 3 7
58 6 4 3 7
59 6 4 3 7
60 6 4 3 7
61 6 4 3 7
62 6 4 3 7
63 6 4 3 7
64 6 4 3 7
65 6 4 3 7
66 6 4 3 7
67 6 4 3 7
68 6 4 3 7
69 6 4 3 7
70 6 4 3 7
71 6 5 2 7
72 6 5 2 7
73 6 5 2 7
74 6 5 2 7
75 6 5 2 7
76 6 5 2 7
77 6 5 2 7
78 6 5 2 7
79 6 5 2 7
80 6 5 2 7
81 6 6 1 7
82 6 6 1 7
83 6 6 1 7
84 6 6 1 7
85 6 6 1 7
86 6 6 1 7
87 7 7 0 7
88 7 7 0 7
89 7 5 3 8
90 7 5 3 8
91 7 5 3 8
92 7 5 3 8
93 7 5 3 8
94 7 5 3 8
95 7 5 3 8
96 7 5 3 8
97 7 5 3 8
98 7 5 3 8
99 7 5 3 8
100 7 5 3 8
101 7 5 3 8
102 7 5 3 8
103 7 6 2 8
104 7 6 2 8
105 7 6 2 8
106 7 6 2 8
107 7 6 2 8
108 7 6 2 8
109 7 6 2 8
110 7 6 2 8
111 7 6 2 8
112 7 6 2 8
113 7 7 1 8
114 7 7 1 8
115 7 7 1 8
116 7 7 1 8
117 7 7 1 8
118 7 7 1 8