на компактном метрическом пространстве

сходящаяся к непрерывной функции

А зачем здесь метрическое пространство? Думаю, можно немножко "облегчить" доказательство (убрать все эти индексированные эпсилон итд).
Чистая компактность. Фиксируем

. Для всякой точки

найдется

такое, что

. В силу непрерывности

это неравенство выполняется и в некоторой открытой окрестности

. Ну и все. Из открытого покрытия выбираем конечное подпокрытие. Для каждого множества свой номер

, берем максимум. Начиная с этого номера уже для любой точки

выполнено неравенство
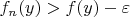
.
Любопытно отметить, что в приведенном доказательстве, ВРОДЕ БЫ, не используется предположение, что

непрерывна. Меня это как-то смутило. Но это, разумеется, не так. Прикольно.



