Задача на соленоид

[tupoy_vopros]

На рисунке условие и решение задачи из пособия Иродова "Основные законы электромагнетизма"
В прошлой своей теме я уточнял, что в теореме о циркуляции магнитного поля по контуру важен именно ток, а не его проекция (проекции линейной плотности) на площадку, которая натянута на контур.
Тут же именно раскладывают ток на две составляющие. Можно ли тут так делать ? Почему использовать просто модуль тока $i$ будет ошибкой ?

[Cos(x-pi/2)]

Извините, но похоже, что Вы всё-таки не поняли как следует объяснений в той теме. Попробуйте вернуться к основам - ещё раз внимательно обдумайте вычисление выражения $\int_S \,\mathbf{j}\cdot d\mathbf{S}.$

(Напоминания:)

Жирными буквами обозначаются векторы. $d\mathbf{S}$ это тоже вектор. Точка между векторами означает скалярное произведение (бывает, для краткости эту точку не пишут, но тогда она подразумевается):

$\mathbf{A}\cdot\mathbf{B}=A_xB_x+A_yB_y+A_zB_z=A\,B\,\cos\alpha,$

где: $\alpha$ - угол между векторами $\mathbf{A}$ и $\mathbf{B},$

$A=|\mathbf{A}|=\sqrt{A_x^2+A_y^2+A_z^2}\,,$
$B=|\mathbf{B}|=\sqrt{B_x^2+B_y^2+B_z^2}\,.$

$S$ у знака интеграла означает ориентированную поверхность, $d\mathbf{S}=\mathbf{n}\,dS$ - вектор элемента площади $dS$ на этой поверхности, $\mathbf{n}$ - единичный вектор нормали этого элемента площади (нормаль это перпендикуляр к элементу площади). Слово "единичный" здесь означает, что $\mathbf{n}\cdot\mathbf{n}=1.$

Заданную поверхность $S$ можно представлять себе в виде "мозаики", составленной из бесконечно малых элементов площади $dS,$ из которых торчат их векторы нормалей $\mathbf{n}.$ Из каждого элемента площади торчит ещё и вектор $\mathbf{j},$ картина таких векторов это векторное поле $\mathbf{j},$ рассматриваемое на поверхности $S.$

Локально, в месте расположения каждого элемента площади мы вычисляем скалярные произведения

$$\mathbf{j}\cdot d\mathbf{S}=\mathbf{j}\cdot\mathbf{n}\,dS = j\,\cos\alpha\,dS\,, $$

где $\alpha$ - угол между векторами $\mathbf{j}$ и $\mathbf{n}$ в данном месте. И суммируем получившиеся числа по всем элементам, т.е. по всей заданной поверхности $S.$ Эта сумма и есть $\int_S \,\mathbf{j}\cdot d\mathbf{S}.$

Разберём простейшие примеры. Пусть поверхность $S$ - плоская. Тогда все векторы $\mathbf{n}$ одинаково направлены, не изменяются от элемента к элементу. Пусть поле $\mathbf{j}$ - однородное, т.е. векторы $\mathbf{j}$ не изменяются от точки к точке в пространстве. Тогда $\mathbf{j}\cdot\mathbf{n}$ есть постоянная величина, можно её вынести из под знака интеграла; оставшийся интеграл равен просто площади $S$ заданной поверхности. Т.е. в таких частных случаях имеем:

$$\int_S \,\mathbf{j}\cdot d\mathbf{S}=(\mathbf{j}\cdot\mathbf{n})\int_SdS=(\mathbf{j}\cdot\mathbf{n})\,S.$$

Упражнение:

Дано (в соответствующих физических единицах измерения, но для краткости единицы измерения не выписываю): во всей рассматриваемой области 3-мерного пространства $j_x=0,$ $j_y=3,$ $j_z=4,$ Найти $\int_S \mathbf{j}\cdot d\mathbf{S}$ для плоской поверхности в виде прямоугольника, если у этого прямоугольника:

а) нормаль - вдоль оси $x,$ длины сторон: $\Delta y=2,$ $\Delta z=1;$
б) нормаль - вдоль оси $y,$ длины сторон: $\Delta x=6,$ $\Delta z=5;$
в) нормаль - вдоль оси $z,$ длины сторон: $\Delta x=1,$ $\Delta y=2;$

Когда справитесь с этим, можно будет разобрать простые примеры с неоднородным полем $\mathbf{j},$ в том числе с проводом конечного сечения из предыдущей темы и с лентой из данной темы.

[мат-ламер]

tupoy_vopros в сообщении #1680612 писал(а):

В прошлой своей теме я уточнял, что в теореме о циркуляции магнитного поля по контуру важен именно ток, а не его проекция (проекции линейной плотности) на площадку, которая натянута на контур.

Если у вас контур охватывает соленоид, то через этот контур течёт только та составляющая тока, которая течёт вдоль соленоида. Та составляющая, которая описывает круги и не перемещается вдоль соленоида, через контур не проходит.

[мат-ламер]

tupoy_vopros в сообщении #1680612 писал(а):

В прошлой своей теме я уточнял, что в теореме о циркуляции магнитного поля по контуру важен именно ток, а не его проекция (проекции линейной плотности) на площадку, которая натянута на контур.

В прошлой теме у вас был вектор тока, который либо проходит через наш контур целиком, либо нет. Смотрите там в конце аналогию с струёй воды и ведром. В этой теме у нас вектор плотности тока образует векторное поле. И оно не обязано целиком проходить через контур. Смотрите в прошлой теме аналогию с дождём и ведром воды. Тут мы вычисляем поток векторного поля через поверхность.

[мат-ламер]

мат-ламер в сообщении #1680702 писал(а):

В прошлой теме у вас был вектор тока, который либо проходит через наш контур целиком, либо нет. Смотрите там в конце аналогию с струёй воды и ведром.

Более внимательно посмотрел прошлую тему. И что-то я засомневался в том, о чём там написано. Вектор тока - это для начала вектор. И если есть кусок поверхности, то речь может идти о потоке вектора через эту поверхность, которая вычисляется через понятно какой интеграл от скалярного произведения.

[DimaM]

мат-ламер в сообщении #1680710 писал(а):

Вектор тока - это для начала вектор.

Нет в природе вектора тока. Ток - скаляр.
Есть вектор плотности тока.
В прошлой теме все это хорошо написано, а вы зачем-то опять взялись вводить людей в заблуждение.

[tupoy_vopros]

Cos(x-pi/2)
a)0
b)$ 3\cdot6\cdot5 = 90 $
c)$ 4\cdot1\cdot2 = 8 $

[tupoy_vopros]

Разобрался
циркуляция прямоугольника, обхватывающего поверхность соленоида равна $B l$, и она равна $I$
В тоже время $I = i_{perp}l = I h $
Собственно $l$ зависит от угла. И $B$ зависит от угла. В целом циркуляция постоянна и противоречия нет.
Собственно это amon и писал касательно площади

[Cos(x-pi/2)]

tupoy_vopros
Ответы правильные. (Пожелание: лучше сначала писать решения "в буквах", т.е. в виде выражений, и только в самом конце подставлять в них числовые значения букв. Тогда будет видно, как получаются ответы и почему они разные (или одинаковые) в разных задачках. Если Вы так и делаете в своих вычислениях, то хорошо.)

Вижу, Вы уже разобрались, пока я подготавливал следующее упражнение. Ну, тогда пусть оно тут останется на всякий случай; если Вам оно не надо, то и не делайте его.

(Следующее упражнение:)

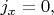
Дано: теперь векторное поле $\mathbf{j}$ пусть равно нулю в каждой точке пространства вне провода с прямоугольным поперечным сечением. Размеры поперечного сечения провода: $a=3,$ $b=2$ (в единицах длины). Внутри провода векторное поле $\mathbf{j}$ отлично от нуля: пусть там в каждой точке мы имеем $j_x=0,$ $j_y=3,$ $j_z=4$ (в единицах плотности тока).

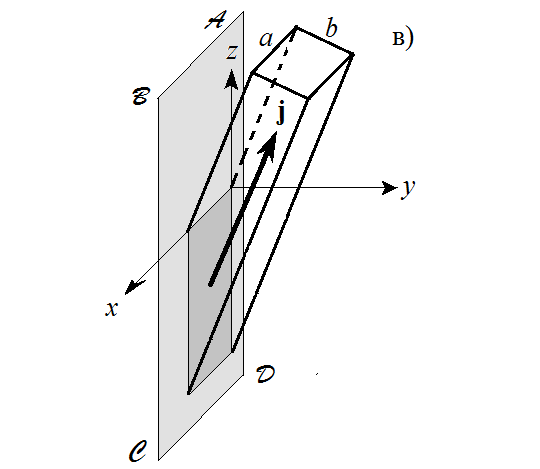
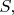
Провод длинный, но на рисунках ниже для простоты изображены только кусочки этого провода. Показаны три варианта пересечения провода воображаемой плоской прямоугольной поверхностью $S,$ её граничный контур АBCD окружает провод. Найти $\int_S\, \mathbf{j}\cdot d\mathbf{S}$ в случаях:

а) поверхность $S$ перпендикулярна к $\mathbf{j}$ в проводе; её нормаль направлена вдоль $\mathbf{j}:$




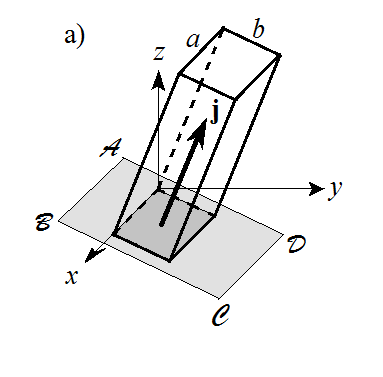
б) нормаль $\mathbf{n}$ поверхности $S$ направлена вдоль оси $z,$ т.е. $n_x=n_y=0,$ $n_z=1:$




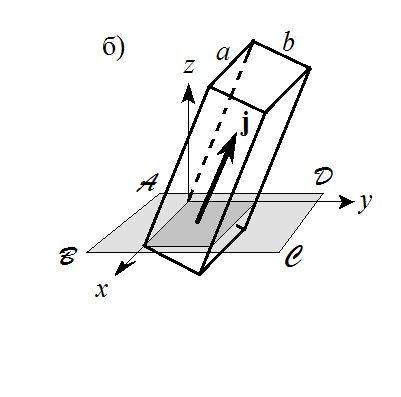
в) нормаль $\mathbf{n}$ поверхности $S$ направлена вдоль оси $y,$ т.е. $n_x=n_z=0,$ $n_y=1:$

Добавил 04.04.2025 для полноты:

(Заключительное упражнение)

Представим себе следующую картину. Пусть такое же ненулевое векторное поле $\mathbf{j},$ как в проводе из примера выше, было задано внутри большой пластины толщиной $a,$ и эту пластину изогнули (вместе с векторным полем $\mathbf{j}$ в ней) так, что получилась труба с толщиной стенки $a.$ Часть этой трубы схематично показана ниже на рисунках.

Толщину трубы $a$ считаем малой, так что площадь поперечного сечения стенки трубы, т.е. площадь кольца с внутренним радиусом $R_1$ и внешним радиусом $R_2=R_1+a,$ достаточно вычислять приближённо: $\pi(R_2^2-R_1^2)\approx 2\pi R_1a.$ Радиус $R_1$ и $a$ - заданные параметры.

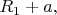
Поле $\mathbf{j}$ в полости трубы и снаружи трубы равно нулю. В стенке трубы, т.е. в точках пространства, находящихся от оси $y$ на расстояниях $R=\sqrt{x^2+z^2}$ больших, чем $R_1,$ но меньших, чем $R_1+a,$ поле $\mathbf{j}$ описывается формулами:

$$j_x=-j_1\,\dfrac{z}{R},$$

$$j_z=j_1\,\dfrac{x}{R},$$

$$j_y=j_2,$$

где $j_1$ и $j_2$ это заданные постоянные с размерностью плотности тока. (В задаче Иродова им соответствуют компоненты "линейной плотности тока" $i_{\perp}=j_1 a,$ и $i_{||}=j_2 a.)$


Требуется для двух вариантов найти (выразить через заданные постоянные) величину $\int_S\,\mathbf{j}\cdot d\mathbf{S},$ где $S$ - плоская поверхность, ограниченная прямоугольным контуром ABCD; см. рисунки ниже. Ориентация поверхности задаётся нормалью $\mathbf{n}:$

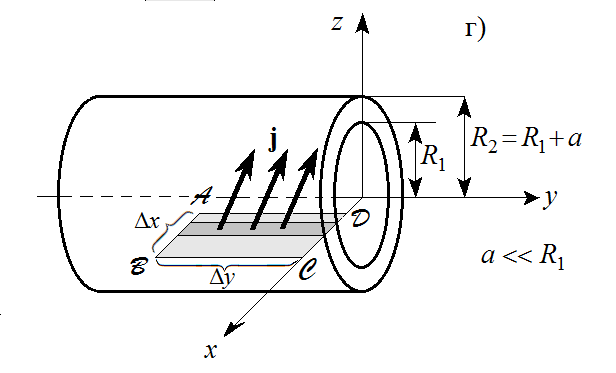
г) $n_x=n_y=0,$ $n_z=1.$ Размеры прямоугольника ABCD заданы, это $\Delta x$ и $\Delta y:$




д) $n_x=n_z=0,$ $n_y=1.$ Подразумевается, что размеры $\Delta x$ и $\Delta z$ прямоугольника ABCD заданы:



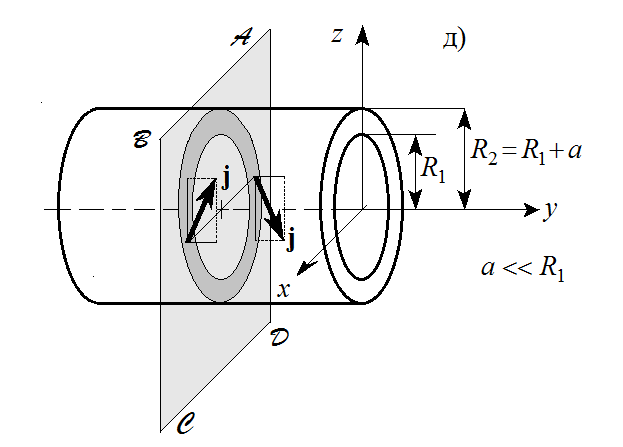
Для наглядности в нескольких точках изображены векторы плотности тока $\mathbf{j}.$


Дополнительные вопросы:

e) Изменится ли ответ в случае д) если в роли $S$ вместо прямоугольника выбрать круг с центром на оси $y$ c радиусом $R,$ превышающим внешний радиус трубы $R_2?$

ж) Представим себе, что труба с указанным выше полем плотности тока $\mathbf{j}$ изготовлена намоткой проводящей ленты, как в задаче Иродова. Найти ширину ленты $h$ и силу тока в ленте $I.$

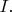
(Решения)

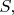
Во всех заданных для рассмотрения случаях в тех точках поверхности $S,$ в которых величина $\mathbf{j}\cdot\mathbf{n}$ отлична от нуля, она оказывается постоянной и поэтому может быть вынесена из под знака интеграла:

$$\int_S \,\mathbf{j}\cdot d\mathbf{S}\,=\,(\mathbf{j}\cdot\mathbf{n})\,S\,,$$

где $S$ - площадь того участка заданной поверхности, на котором $\mathbf{j}\cdot\mathbf{n}\neq 0.$ На рисунках такой участок поверхности закрашен тёмным серым цветом.


a) $\mathbf{j}\cdot\mathbf{n}=j,$ где $j=\sqrt{j_x^2+j_y^2+j_z^2}=\sqrt{0^2+3^2+4^2}=5$ единиц плотности тока.

$S=ab=3\cdot 2=6$ единиц площади.

Ответ: $(\mathbf{j}\cdot\mathbf{n})\,S\,= j\,ab.$ Это сила тока $I$ в проводе; численный ответ: $I=5\cdot 6=30$ единиц силы тока.


б) $\mathbf{j}\cdot\mathbf{n}=j_zn_z=j_z=j\,\cos\alpha,$ где $\alpha$ - угол между осью $z$ (вдоль неё направлен вектор $\mathbf{n})$ и вектором $\mathbf{j}.$

$S=a\,\dfrac{b}{\cos\alpha}.$

Ответ: $(\mathbf{j}\cdot\mathbf{n})\,S\,= \,j\,ab\,=\,I.$


в) $\mathbf{j}\cdot\mathbf{n}=j_yn_y=j_y=j\,\cos\alpha,$ где $\alpha$ - угол между осью $y$ (вдоль неё направлен вектор $\mathbf{n})$ и вектором $\mathbf{j}. $

$S=a\,\dfrac{b}{\cos\alpha}.$

Ответ: $(\mathbf{j}\cdot\mathbf{n})\,S\,= \,j\,ab\,=\,I.$


г) $\mathbf{j}\cdot\mathbf{n}=j_1,$

$S=a\,\Delta y.$

Ответ: $(\mathbf{j}\cdot\mathbf{n})\,S\,= \,j_1 a\,\Delta y.$


д) $\mathbf{j}\cdot\mathbf{n}=j_2,$

$S=2\pi R_1 a$ (приближённо).

Ответ: $(\mathbf{j}\cdot\mathbf{n})\,S\,= \,2\pi R_1 a\,j_2.$


e) В варианте с кругом радиуса $R>R_1+a$ ответ такой же: $2\pi R_1 a\,j_2$ (приближённо).


ж) С помощью изображения ленты, подобного приведённому в задаче Иродова, получается ответ для ширины ленты:

$h=2\pi R_1\dfrac{j_2}{j},$

где $j=|\mathbf{j}|=\sqrt{j_1^2+j_2^2}.$

Сила тока в ленте $I$ равна плотности тока $j,$ умноженной на площадь поперечного сечения ленты:

$I=j\,a\,h=2\pi R_1a\,j_2\,.$

Параметры $j_1$ и $j_2$ теперь можно выразить через $h,\,I,$ радиус соленоида $R_1$ и толщину ленты $a:$

$$j_2=j\,\frac{h}{2\pi R_1}=\frac{I}{2\pi R_1a}\,,$$

$$j_1=\sqrt{j^2-j_2^2}=j\sqrt{1-(j_2/j)^2}=\frac{I}{ha}\sqrt{1-(h/2\pi R_1)^2}\,.$$

При этом ответ г) запишется в виде

$$j_1 a\,\Delta y = \Delta y\,\frac{I}{h}\sqrt{1-(h/2\pi R_1)^2}$$

Это выражение согласно "теореме о циркуляции"

$$\oint_{\partial S}\,\mathbf{B}\cdot d\mathbf{r}=\mu_0\int_S\,\mathbf{j}\cdot d\mathbf{S}$$

(где $\partial S$ есть обозначение границы ориентированной поверхности $S)$ вместе с дополнительными соображениями о картине магнитного поля даёт формулу для магнитного поля $B_{||}=|B_y|$ внутри соленоида:

$$B_{||}\,\Delta y = \mu_0 \,\Delta y\,\frac{I}{h}\sqrt{1-(h/2\pi R_1)^2}$$

Ответ е) запишется в виде

$$2\pi R_1 a\,j_2=I\,.$$

Умноженное на $\mu_0$ это выражение равно циркуляции магнитного поля по окружности $\partial S$ радиуса $R>R_1+a.$ Таким образом вместе с дополнительными соображениями о картине магнитного поля снаружи соленоида для величины этого поля $B_{\perp}$ получается формула:

$$2\pi R\,B_{\perp}=\mu_0 I\,.$$