Неизометричность компакта собственному подмножеству

[drzewo]

Ende
Выделено из темы «Группа не изоморфна собственной подгруппе».

Задача для ТС
Доказать, что компактное метрическое пространство $X$ не может быть изометрически изоморфно своему подпространству $F\subset X,\quad F\ne X$

[StudentV]

Здравствуйте, drzewo. Спасибо за задачу.

Думаю, ход решения должен быть такой:
- компактное метрическое пространство $X$ вполне ограничено. Это значит, что для любого $\varepsilon>0$ найдется конечное множество $N \subset X$ такое, что $\forall x \in X \exists n \in N \colon \rho(x, n) \le \varepsilon$. Это множество $N$ называется $\varepsilon$-сетью.
- нужно взять граничную точку $x$ множества $F$
- предположим, что существует изометрия $f \colon X \to F$
- нужно показать, что найдется $\varepsilon$ и соответствующая ему точка $n$ из $\varepsilon$-сети, для которых условие $\rho(f(x), f(n)) \le \varepsilon$ противоречит неравенству треугольника.

Полное доказательство придумать не смог, но еще подумаю. Буду благодарен, если подскажете, в правильном ли направлении я думаю.

[drzewo]

Классическая задача, вот мое решение.
https://storage4u.ru/file/2025/03/29/7d94bc051c6ab85256b08751130c8a3f.pdf

[StudentV]

Уважаемый drzewo, спасибо за решение. К сожалению, я не понял обозначения $f^n(z)$. Это что - $\underbrace{f \circ f \dots \circ f}_n$, т.е. $n$-кратная композиция функции с собой, или что-то другое?

[drzewo]

да, это композиция. Последовательность $f^n(z)$ содержит подпоследовательность Коши -- в силу компактности

[StudentV]

Уважаемый drzewo, спасибо, теперь я понял Ваше изящное доказательство. Конечно, сам я не додумался бы до него.

Интересно, можно ли обобщить доказанное утверждение на некомпактные, но вполне ограниченные пространства? Ваше доказательство существенно опирается на компактность, которая сильнее полной ограниченности: по лемме Гейне-Бореля, компактность = полная ограниченность + полнота.
Выше я попытался придумать доказательство, опирающееся только на полную ограниченность, но не преуспел. Моя неудача, конечно, ничего не означает. Но все-таки любопытно, есть ли пример вполне ограниченного пространства, изометричного собственному подпространству.

[dgwuqtj]

StudentV в сообщении #1680506 писал(а):

Но все-таки любопытно, есть ли пример вполне ограниченного пространства, изометричного собственному подпространству.

Есть. Возьмём множество $\{(\cos n \theta, \sin n \theta) \mid n \geq 0\} \subseteq \mathbb S^1$, где $\theta$ иррациональный угол (то есть все точки $(\cos n \theta, \sin n \theta)$ попарно различны). Оно изометрично собственному подпространству $\{(\cos n \theta, \sin n \theta) \mid n \geq 1\}$, изометрия — это поворот на $\theta$.

[vpb]

Можно исходную и через $\varepsilon$-сети решить. Но надо еще понятие $\varepsilon$-разреженного множества, т.е. такого, что между любыми его точками расстояние $>\varepsilon$.

Лемма. Если есть $\varepsilon$-сеть из $M$ точек, то для любого $\delta>2\varepsilon$ любое $\delta$-разреженное множество содержит не больше чем $M$ точек. (Доказать самому).

Следствие. Для данного $\varepsilon$ существует $N$ такое, что любое $\varepsilon$-разреженное множество содержит не более чем $N$ точек.

Теперь рассуждаем так. Пусть $f$ --- изометрическое вложение компакта $K$ в себя. Если $f(K)\ne K$, то есть точка $x\notin f(K)$. Возьмем $\varepsilon< d(x, f(K))$. Возьмем в $K$ некоторое $\varepsilon$-разреженное множество $X$ из максимально возможного числа точек, скажем из $M$ точек. Тогда $f(X)$ --- тоже $\varepsilon$-разреженное, из $M$ точек. Но $x$ лежит от $f(K)$, а тем более от $f(X)$, на расстоянии $>\varepsilon$. Значит $f(X)\cup\{x\}$ --- $\varepsilon$-разреженное из $M+1$ точки, противоречие.

[drzewo]

(Оффтоп)

Утверждение, что я выкладывал выше можно несколько обобщить
https://storage4u.ru/file/2025/04/01/cbf3e2cd46a007122c180e6e5e1a669f.pdf

[StudentV]

Уважаемый dgwuqtj, спасибо за пример. К сожалению, я не очень понял его. $S^1$ - это окружность, для задания точки на ней достаточно одной координаты - угла поворота $\varphi$. Я попытался переписать Ваше построение в этой системе координат, но не понял, почему поворот на $\theta$ - изометрия.
Возможно, Вы имели в виду все-таки $S^2$ ?

Уважаемый vpb, спасибо за доказательство. Я попытаюсь его разобрать в ближайшее время.

[dgwuqtj]

StudentV в сообщении #1680605 писал(а):

$S^1$ - это окружность, для задания точки на ней достаточно одной координаты - угла поворота $\varphi$. Я попытался переписать Ваше построение в этой системе координат, но не понял, почему поворот на $\theta$ - изометрия.

Если моё множество записать через полярный угол, будет $\{n \theta \bmod 180^\circ \mid n \geq 0\}$. При прибавлении $\theta$ оно переходит в собственное подмножество.

[StudentV]

Здравствуйте, уважаемые участники форума. Извините, что задержался с ответом, не было возможности ходить на форум.

Уважаемый dgwuqtj, спасибо, теперь Ваш контрпример понятен. Но, я думаю, тут есть описка:

dgwuqtj в сообщении #1680607 писал(а):

Если моё множество записать через полярный угол, будет $\{n \theta \bmod 180^\circ \mid n \geq 0\}$.

Разве не $\bmod 360^\circ$? Ведь метрика должна быть неотрицательной.

Отдельное спасибо за то, что обратили мое внимание на окружность как пример метрического пространства. Этот прием может быть полезен для построения разных контрпримеров.

Уважаемый vpb, спасибо за Ваше изящное доказательство исходного утверждения. По сути, оно опирается на два свойства компактных множеств в метрических пространствах: 1) полную ограниченность 2) замкнутость. Если бы $f(K)$ было не замкнуто, то точка $x$ могла бы находиться на нулевом расстоянии от $f(K)$, и доказательство бы не сработало. Само собой, замкнутость использовалась и в доказательстве уважаемого drzewo.

vpb в сообщении #1680552 писал(а):

Лемма. Если есть $\varepsilon$-сеть из $M$ точек, то для любого $\delta>2\varepsilon$ любое $\delta$-разреженное множество содержит не больше чем $M$ точек. (Доказать самому).

Похоже, я это доказал, хотя и весьма неуклюже. Мне понадобится

Лемма 2. Если есть $\varepsilon$-сеть $S$ из $m$ точек и для некоторого $\delta>2\varepsilon$ найдется $\delta$-разреженное множество $Y$ из $m$ точек, то для каждой точки $y \in Y$ найдется ровно одна точка $s \in S$ такая, что $\rho (s, y) \le \varepsilon$ (разрешите переобозначить количество точек маленькой буквой, чтобы не путать с множествами).

(Доказательство)

По определению $\varepsilon$-сети, для каждой точки $y \in Y$ найдется хотя бы одна такая точка $s \in S$. Нужно доказать, что их не больше.
Начнем со случая $m=2$. Предположим противное: $\rho (s_1, y_1) \le \varepsilon, \ \rho (s_2, y_1) \le \varepsilon$. Тогда из условия $\rho (y_1, y_2) > 2 \varepsilon$ и неравенства треугольника имеем, что $\rho (s_1, y_2) > \varepsilon, \ \rho (s_2, y_2) > \varepsilon$, что противоречит определению $\varepsilon$-сети. Перейдем к случаю $m=3$ в тех же обозначениях. Теперь у нас есть дополнительная точка $s_3$, и по определению $\varepsilon$-сети должно выполняться, что $\rho (s_3, y_2) \le \varepsilon$. Но одновременно появилась и точка $y_3$, и теперь из неравенства треугольника $\rho (s_1, y_3) > \varepsilon, \ \rho (s_2, y_3) > \varepsilon, \ \rho (s_3, y_3) > \varepsilon$. В случае $m = 4$ точка $s_4$ может "спасти" $y_3$, но мы получим те же проблемы для $y_4$, и т.д. Вот это "и т.д.", строго говоря, тоже надо доказывать. Наверное, это можно как-то красиво записать через математическю индукцию, но я не умею.

Вернемся к доказательству основной леммы. Пусть в пространстве есть $\varepsilon$-сеть $S$ из $m$ точек: $\{s_1, \dots s_m\}$. Возьмем $\delta>2\varepsilon$. Если в пространстве нет $\delta$-разреженного множества из $m$ точек, утверждение леммы выполнено. Предположим, что такое множество $Y$ есть. Перенумеруем точки $Y$, исходя из условия $\rho(y_i, s_i) \le \varepsilon$ (мы можем это сделать по лемме 2). Теперь рассмотрим точку $y_{m+1} \notin Y$. По условию, найдется точка $s_i$ такая, что $\rho(s_i, y_{m+1}) \le \varepsilon$. 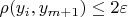Поэтому из неравенства $\rho(y_i, y_{m+1}) \le \rho(s_i, y_i) + \rho(s_i, y_{m+1})$ имеем $\rho(y_i, y_{m+1}) \le 2\varepsilon$, т.е. множество $Y \cup \{y_{m+1}\}$ не является $\delta$-разреженным. ЧТД.

Кстати говоря, мне не удалось построить пример пространства, в котором есть $\varepsilon$-сеть $S$ из $m$ точек и для некоторого $\delta>2\varepsilon$ найдется $\delta$-разреженное множество $Y$ из $m$ точек (как в условии леммы 2). Я верю, что такое возможно, но хотелось бы посмотреть.

[drzewo]

Нате Вам для комплекта
Пусть $(X,\rho)$ -- компактоное метрическое пространство и отображение $f:X\to X$ таково, что

$$\rho(f(x'),f(x''))\le \rho(x',x''),\quad \forall x',x''\in X.$$

Доказать, что если $f(X)=X$ то

$$\rho(f(x'),f(x''))= \rho(x',x''),\quad \forall x',x''\in X.$$

[StudentV]

drzewo в сообщении #1681588 писал(а):

Нате Вам для комплекта

Ой, интересно, но уже боюсь браться. А то еще что-нибудь зададите.

-- 09.04.2025, 18:09 --

StudentV в сообщении #1681587 писал(а):

По сути, оно опирается на два свойства компактных множеств в метрических пространствах: 1) полную ограниченность 2) замкнутость.

В сущности, уважаемый vpb доказал следующее: если $X$ вполне ограничено, $f \colon X \to X$ - изометрия и $f(X)$ замкнуто в $X$, то $f(X) = X$. Случай компактного $X$ - важный, но частный.