Здравствуйте!
Разбираю задачки из НМУ прошлых лет и наткнулся на категорическое непонимание.
Задача 1. Предъявить всюду дифференцируемую функцию (на R) такую, что

,

и не существует окрестностей нуля, на которых эта функция была бы диффеоморфизом.
Я не понимаю, как эта задача согласуется с теоремой об обратной функции, которая по сути и утверждает, что непрерывно-дифференцируемая функция с ненулевой производной обязана быть диффеоморфизом. Единственное условие из формулировки теоремы, которое в условии задачи не требуется - это непрерывность производной, но по условию

всюду дифференцируема, а производная не может иметь точек разрыва первого рода. Точки разрыва второго рода явно запрещены.
Задача 2. Привести пример гладкого векторного поля
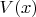
на сфере

в

, заданной уравнением

, такого, что

,

для всех

.
Думаю, очевидно, что здесь возникает вопрос о том, как эта задача согласуется с теоремой о еже.
Помогите, пожалуйста, справиться с троллингом Шапошникова. Спасибо!



