Добрый день. Хочу предложить в обсуждению метод построения асимптотических приближений к общему решению произвольной линейной системы обыкновенных дифференциальных уравнений с переменными коэффициентами и малым параметром при старших производных. Я буду рад любым критическим замечаниям, а также указанием на похожие идеи у других авторов, потому что я пока не знаю - исследовал кто-либо нечто подобное или нет.
Сперва продемонстрирую мой подход на нескольких простых примерах, а потом постараюсь сказать пару слов об общем случае. Итак, рассмотрим уравнение Эйри

где

- некий малый параметр, а

- неизвестная функция. Общее решение этого уравнения хорошо известно

что позволит нам впоследствии проверить качество полученных нами приближений. Здесь

и

- произвольные постоянные, а

и

- функции Эйри первого и второго рода. Но предположим на минуточку, что общее решение нам неизвестно и зададимся целью построить его асимптотическое приближение по малому параметру

.
Основная идея, с помощью которой мы будем пробовать это делать будет состоять в "диагонализации" исходного уравнения, что означает его расщепление на пару независимых уравнений

где

и

- какие-то неизвестные функции, которые определяют как оператор дифференцирования действует на два линейно независимых решения исходного уравнения. Но поскольку нас интересует не точное решение, а лишь его приближение, то и функции

и

будем искать не в точности, а в виде некоторого ряда по степеням параметра

.
Однако степень первого члена в этих рядах для

и

будем выбирать не произвольно, а по следующей процедуре. Заметим, что если бы коэффициенты исходного уравнения были бы постоянными, то функции

и

совпадали бы с собственными числами соответствующего уравнения, а потому и в нашем случае первое приближение к

и

будем искать из уравнения на "собственные числа"

откуда

Здесь возникает тонкий момент, ведь пространство распадается на две области - для положительных значений

квадратный корень извлекается тривиально, а для отрицательных - с мнимой единицей. Но это в известной степени неизбежно, потому что функции Эйри по разному ведут себя на плюс и минус бесконечности, а значит перед нами будет стоять проблема состыковки двух типов решений.
Тем не менее продолжим. Полученное выражение для

хоть и является нулевым приближением, но тем не менее оно совсем не удовлетворительно (если подставить его в исходное уравнение, то лишь при самой старшей степени

получится верное равенство), поэтому будем его уточнять. Для примера покажем как это сделать для положительной ветви квадратного корня. Будем искать

в следующем виде

где

- некоторая функция. Тогда

и, стало быть,

Подставляя это выражение в исходное уравнение и приравнивая коэффициенты при первых двух старших степенях

находим, что

Точно таким же образом можно убедиться, что для случая, когда

ответ получается точно таким же. Таким образом, в первом приближении общее решение исходной системы для положительных значений

можно найти как произвольную линейную комбинацию решений двух независимых уравнений

То есть

что совпадает с известной асимптотикой для функций Эйри в окрестности бесконечности. Действительно, при

справедливо представление

что означает, что построенные нами приближенное решение с учетом наличия произвольных постоянных - оказалось верным. В принципе те же самые рассуждения можно повторить для области с отрицательными значениями

, где квадратный корень для собственных значений будет раскрываться с мнимой единицей и будут, соответственно, получаться тригонометрические, а не экспоненциальные решения. Но я не хочу перегружать сообщение техническими моментами, и поэтому позволю себе перейти ко второму примеру уже для конкретно системы уравнений
Итак, рассмотрим систему уравнений

общее решение которой имеет вид

где

и

- это функции Бесселя первого и второго рода с соответствующим нижним индексом.
Будем искать асимптотическое приближение сходным образом. Сперва найдем собственные числа для матрицы

откуда

. Теперь для каждого из этих значений по отдельности будем искать асимптотическую диагонализацию по параметру

. По традиции в явном виде сделаю это для положительного значения корня, а для отрицательного - потом сразу приведу результат, чтобы не перегружать сообщение однотипными вычислениями. Итак, пусть

тогда подставим эти выражения в исходную систему

откуда, собирая слагаемые при главных степенях по

, найдем

Чтобы найти сам вид

нам потребуется перейти к дифференциальным следствиям из полученных нами уравнений. Так, дифференцируя выражение для
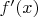
находим

а дифференцируя первое уравнение исходной системы получаем

где мы учли, что

и

Объединяя два выражения для

, раскрывая скобки и приравнивая члены при главных степенях

, находим что

. Проводя аналогичные вычисления для отрицательного значения корня можно найти, что там функции

и

будут такими же. Итак общее решение исходной системы должно быть примерно равно сумме решений двух диагональных систем уравнений

то есть

где я прошу меня простить за небольшую перегрузку по значениям произвольных постояний

и

, которую я допустил, выделяя тригонометрический вид решения, но я надеюсь, что всем итак всё будет понятно. Теперь давайте проверим правильно ли у нас получилось. Воспользуемся асимптотиками

и

откуда можно найти, что полученное решение в целом правильное, но там есть какая-то небольшая проблема со структурой произвольных постоянных.
В целом - я изложим общую схему на двух примерах. Понятно, что все это походит на какую-то версию WKB метода и на что-то невероятное я не претендую, но мне интересно ваше мнение.



