За рисунок не взялся (нет удобной рисовалки), поэтому так.
ОБОЗНАЧЕНИЯ.

продлим за т.

до т.

так, что


продлим за т. P

так, что


и

пересекаются в т.

Продолжение

и срединный перпендикуляр к
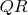
(идёт из т.

) пересекаются в т.

Продолжение

и срединный перпендикуляр к

(идёт из т.

) пересекаются в т.


НАХОДИМ УГЛЫ

(т.к.

- окружность)

(т.к.

- окружность)

(т.к.

- окружность)
Получили

, т.е.

- окружность, поэтому

Теперь утверждение задачи (

) следует из равенства треугольников

и

(по двум сторонам и углу между ними).
Действительно,

,

- общая,




