Задачк на оптимизация плюс урвнение Лапласа

[Pavia]

Есть курсове задание определить оптимальну толщину стенки изоляции.

Рассчет предлогается провест, как расписано в книге Зарубин В.С. Оптимальная толщина охлаждения стенки. 1970 год Книге нет. В боле позних изданиях не все ясно так как ссылки идут на другии книги в часности на эту старую.

Есть пластина подверженная нагреву. К внешней термо изоляции подвден поток.
$q(r)=q_0*exp(-k^2*r^2)$



Вычитал в другой книге что $T_1$ температура среды объмен стенки со средой идет как $a_kT_1$

Уравнене Лапласа в цилиндрической системе координат.определяет расределение температуры.

$T_{rr}(r,z)+1/r*T_r(r,z)+T_{zz}(r,z)=0$

$-{lamda }T_z(r,0)+a_kT(r,0)=a_kT_1$
${lamda }T_z(r,h)=q(r)$
$T_r(0,z)=T_r(\infty ,z)=0$

Дальше предлогается решать используя разделения переменных
$T(r,z)=R(r)*Z(z)$

$R_{rr}(r)+1/rR_r(r)+p^2*R(r)=0$
$Z_{zz}(z)-p^2*Z(z)=0$

p-переменняа разделения.
Решение ищеться ввиде

$R(r)=C_1*J_0+C_2*Y_0$
$Z(z)=D_1*ch(p*z)+D_2*sh(p*z)$

J_0 и Y_0 функции Бесселя.

$C_2=0$
$D_2=D_1*a_k/(lamda *p)$

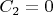
Тут вопрос дальше говориться что p непреывна в приделах 0 бесконечность!! Вопрос почему?
Я смотрел Форонов справчник инженера математика. Так вот там почемуто берется p=0,1,2...
А тут непрерывна и пишется интеграл. А если целые то сумма.
А еще вопрос может нам только одно p нужно?

Дальше вопросов больше.
Решение
$T(r,z)-T1=\int{A(p)*J_0(p*r)*(ch(p*z)+a_k/(lamda *p)*sh(p*z))} dp$

$A(p)=C_1*D_1$ не зависит от координат а только от p
Дальше предлогается взять преобразование Фурье- Бесселя от $q(r)$ и тем самым найти $A(p)$

Тут вопрос каким оброзом k в экспоненте поменяло степень $exp(-k^2*r^2)$ стало $exp(-(p/2k)^2)$

Дальше ищется оптимальная толщина изходя из того что берем температуру в безразмерной велечене. $v=(T(0,h)-T_1)/(q_0*/(lamda*k^2))$

Тут вопрос, больше по физике получается что h не зависит от T_1 и q_0 ? Странно это.

Оптимальная толщина будет при $dv/dh=0=1/2\int{((a_k/lama)^2-p^2)/(p*ch(p*h)+a_k/lamda*sh(p*h))*exp(-(p/(2*k))^2)d(p/k)}$ вот тут дальше непонятки как и откуда что получается. Тут идет ссылка на книжку которой у меня нет (та книга 1970 года).
Может кто поможет решить? Там говориться что такое возможно только при
a_k/(lama*k)<2 вот тут непонятно как это взялось???
Откуда $h=Bi*a_k/lama$ Bi - критерий Био из графика Bi=0.9, но хочется иметь формулу может кто подскажет???
Получается h=0.09 можно ли считать такое h стримящимся к нулю? Или это неважно

Преподователь говорит взять (a_k/lama)^2-p^2=0 откуда найти p, но тут я сомниваюсь.

Пробовал считать численно инеграл. Но тут бесконечность и сходимость плохая. 0.27

[Pavia]

Хотяб чтони-будь подскажите. А то препод сам не понимат, а сдать надо.

[V.V.]

А зачем в полярных координатах переписывать? Что, если решить в прямоугольных задачу в полосе между плоскостями? И явный вид решения дифференцировать по $h$ и т.д.?