Note: the problem is from Fillipov's Problems in Differential Equation Q.631, suggested by a user on thiis very site overr an year ago, and the form of vvariattion of parramter I'm uusiing here is given in Tenenbaum's Ordinary Differential Equations.
I have to solve:
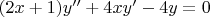
Since, we’re not given any solution, we cannot directly use the method of variations of parameter. After using trial and error method I found

to be one of the solutions.
Method of Variation of Parameters:
Let the general solution be
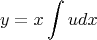
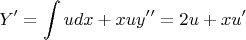
Substituting these values back in the original equation yields:
![$$
x(2x+1)u’ + [2(2x+1) +4x^2] u = 0 \\
x(2x+1) u’ = -(4x^2+4x+2)u \\
u= C[(2x+1)/x^2] \cdot e^{-(2x+1)}
$$ $$
x(2x+1)u’ + [2(2x+1) +4x^2] u = 0 \\
x(2x+1) u’ = -(4x^2+4x+2)u \\
u= C[(2x+1)/x^2] \cdot e^{-(2x+1)}
$$](https://dxdy-02.korotkov.co.uk/f/5/6/7/5673d57cc732f17b590bc5256e192a0182.png)
But to get the general solution I have to integrate

, and it turns out that

is not integrable in terms of elementary functions. Actually, this situation is arising in almost all problems involving Variation of Parameters, and this one is only a paragon of it. Can someone please guide me?