Solving ODE using variation of parameters.

[Knight2023]

Note: the problem is from Fillipov's Problems in Differential Equation Q.631, suggested by a user on thiis very site overr an year ago, and the form of vvariattion of parramter I'm uusiing here is given in Tenenbaum's Ordinary Differential Equations.

I have to solve:
$(2x+1) y'' +4xy' -4y=0$

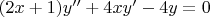
Since, we’re not given any solution, we cannot directly use the method of variations of parameter. After using trial and error method I found $y=x$ to be one of the solutions.

Method of Variation of Parameters:


Let the general solution be



$$ y= x \int u dx $$

$$ Y’= \int u dx + xu \\ y’’ = 2u + xu’ $$

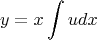
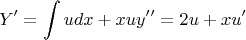
Substituting these values back in the original equation yields:

$$ x(2x+1)u’ + [2(2x+1) +4x^2] u = 0 \\ x(2x+1) u’ = -(4x^2+4x+2)u \\ u= C[(2x+1)/x^2] \cdot e^{-(2x+1)} $$

But to get the general solution I have to integrate $u$, and it turns out that $u$ is not integrable in terms of elementary functions. Actually, this situation is arising in almost all problems involving Variation of Parameters, and this one is only a paragon of it. Can someone please guide me?

[drzewo]

And what guidance do you expect? Yes, sometimes solutions to ODE are not expressed in terms of elementary functions and this does not depend on the method you use to solve the equation

[Knight2023]

drzewo
The method of variation of parameters is in itself a very cumbersome process, involving many intermediate delicate steps, and in the end it is found that general solution is not expressible in elementary form. Was it like this only when you were studying ODEs?

[Ende]

Тема перемещена из форума «Математика (общие вопросы)» в форум «Помогите решить / разобраться (М)»
Причина переноса: в профильный раздел.