Вращающаяся система отсчета в СТО

[epros]

Poehavchij в сообщении #1644103 писал(а):

Т.е. то что я называю "классической" формулой для перехода к вращающейся системе отсчета, она и в ОТО описывает переход к вращающейся системе отсчета ?

Система отсчёта - это сугубо физическое понятие, привязанное к понятиям о том, что именно и как мы будем "отсчитывать" в реальном эксперименте. Строгое его математическое определение может иметь нюансы. Так что лучше пользоваться достаточно строго математически определённым понятием системы координат, которое ему во многом соответствует, не считая тех самых нюансов.

Poehavchij в сообщении #1644103 писал(а):

Просто я думал что там нужно использовать что-то вроде "сопутствующей" системы отсчета ( это скорее всего не то что имейте ввиду Вы когда написали это слово). Мол рассматривать вращающуюся точку и в каждый момент времени использовать преобразование Лоренца по отношению к сопутствующей системе отсчета, т.е. та которая движется в данный момент времени с той же скоростью и в том же направлении что и вращающаяся точка, и так найти, например время. Ну, так по крайней мере в СТО искалось время, которое проходит в равноускоренном космическом корабле

Если мировая линия тела совпадает с осью времени, это уже значит, что координаты сопутствуют телу. Вы же хотите, чтобы координаты ещё и локально совпадали с координатами локально сопутствующей ИСО, что невозможно обеспечить во всех точках пространства-времени.

[sergey zhukov]

Poehavchij
Не рекомендую в это углубляться. Понятие СО связано с материей, т.е. это множество часов, каждые из которых отмечают в своей окрестности местное время и являются там неподвижными. Каждым часам приписаны неизменные пространственные координаты (неподвижность), а время на часах является координатным временем. Получается СК, в которой на мировой линии каждых часов все точки пространства-времени имеют постоянные пространственные координаты этих часов и переменную временную координату, равную собственному времени этих часов. Причем все эти часы должны быть изначально синхронизированы между собой. Так получается некоторый особый вид СК, который можно связать с материей. Но есть много СК, которые просто отвязаны от материи и никак не учитывают ее поведение. Это вполне нормальная ситуация.

[epros]

sergey zhukov в сообщении #1644182 писал(а):

время на часах является координатным временем.

Это необязательно.

sergey zhukov в сообщении #1644182 писал(а):

Причем все эти часы должны быть изначально синхронизированы между собой.

А это в большинстве случаев невозможно. В частности, часы на вращающемся теле, если их разместить в цепочку по контуру и попытаться поочерёдно синхронизировать их друг с другом (в стандартном смысле), то после полного обхода контура обнаружим, что время "не сошлось".

Тем не менее, понятие "одновременности" (в каком-то специально определённом нестандартном смысле) всегда полезно.

sergey zhukov в сообщении #1644182 писал(а):

Так получается некоторый особый вид СК, который можно связать с материей.

Связать с материей (в том смысле, что линии фиксированных пространственных координат сопутствуют материи) недостаточно. Для того, чтобы начать что-то "отсчитывать", нужен ряд дополнительных соглашений.

[Mikhail_K]

Poehavchij
И я тоже думаю, что в теории относительности понятие системы отсчёта нигде не нужно, кроме понятия инерциальной системы отсчёта в СТО. А системы координат могут быть любыми.

epros в сообщении #1644189 писал(а):

В частности, часы на вращающемся теле, если их разместить в цепочку по контуру и попытаться поочерёдно синхронизировать их друг с другом (в стандартном смысле), то после полного обхода контура обнаружим, что время "не сошлось".

Вот-вот.

[Poehavchij]

Mikhail_K

Цитата:

И я тоже думаю, что в теории относительности понятие системы отсчёта нигде не нужно, кроме понятия инерциальной системы отсчёта в СТО. А системы координат могут быть любыми.

Все равно это как-то странно. А если я хочу понять как видит мир наблюдатель в ускоряющийся ракете ? Я всегда думал что ОТО как раз для таких случаев и придумано)

-- 26.06.2024, 11:55 --

sergey zhukov
Вы имейте ввиду не углубляться в это ?

Цитата:

И еще на просторах интернета я нашел некие "координаты Борна" как раз для описания вращения диска в рамках СТО. Если кто-то знает литературу по этому то тоже было бы возможно полезно.

Или в целом в понятие СО ?

[Mikhail_K]

Poehavchij в сообщении #1644193 писал(а):

А если я хочу понять как видит мир наблюдатель в ускоряющийся ракете ? Я всегда думал что ОТО как раз для таких случаев и придумано)

ОТО позволяет это рассчитать, причём пользуясь любой системой координат.

Важный момент: даже в СТО система отсчёта какого-то наблюдателя - это не то, как "видит мир" этот наблюдатель. Например, широко известно, что в движущейся системе отсчёта все объекты сокращаются в направлении движения (а сам движущийся объект сокращается в неподвижной системе отсчёта). Однако, наблюдатель на движущемся с близсветовой скоростью объекте не будет наблюдать никакого сокращения, а будет наблюдать поворот объектов.

То, что наблюдатель видит, вычисляется из того, что происходит в его системе отсчёта, с учётом задержки световых сигналов, которые доходят до него с конечной скоростью. Отсюда понятно, что, в общем-то, идея "системы отсчёта", идея "происходящего на самом деле относительно такого-то наблюдателя" - это некая фикция; объективно лишь то, что такой-то наблюдатель видит такую-то картину. Но в СТО такую фикцию удаётся ввести (с помощью процедуры синхронизации часов, расположенных в разных точках, что даёт возможность говорить об одновременности событий, происходящих далеко друг от друга) и она хорошо работает. Ну вот, а в ОТО не удаётся - см. последнее сообщение epros.

[epros]

Mikhail_K в сообщении #1644190 писал(а):

Poehavchij
И я тоже думаю, что в теории относительности понятие системы отсчёта нигде не нужно, кроме понятия инерциальной системы отсчёта в СТО.

Ну, я бы не был столь категоричен. Неинерциальные СО всё же нужны. Хотя бы для того, чтобы обрёл смысл принцип эквивалентности: Силы тяготения локально эквивалентны неинерциальности системы отсчёта (т.е. исчезают при переходе в инерциальную систему отсчёта).

Тут разговорами о системах координат не отделаться, ибо придётся как-то договариваться о том, как мы "отсчитываем" силы тяготения. Ну и многих интегральных величин это касается. Например, энергия нас может интересовать не только в локальном смысле, но и "в целом для системы". А энергия, как известно, зависит от системы отсчёта. Вот и вопрос: Как её считать, если тело отсчёта вращается?

[sergey zhukov]

Poehavchij
Нет, вращающиеся координаты - это интересно и полезно. Имеется ввиду, что не нужно зацикливаться на понятии "система отсчета".

Можно довольно просто узнать, что видит наблюдатель во вращающейся комнате. Возьмем квадратную, вращающуюся по часовой стрелке, комнату. Наблюдатель (красный) стоит посередине одной ее стены и вращается вместе с комнатой. Мы смотрим на это вращение из неподвижной (не вращающейся) СО,. Я хочу узнать, что будет видеть наблюдатель, когда он окажется в нижней точке своего круга, по которому он вращается в этой комнате.

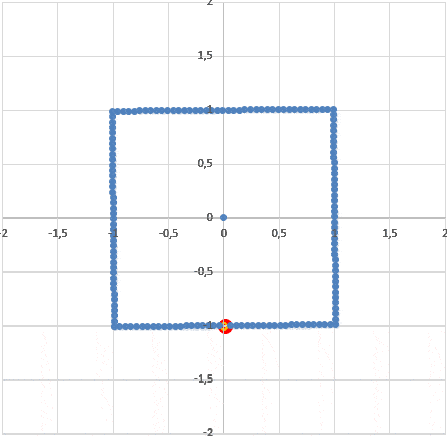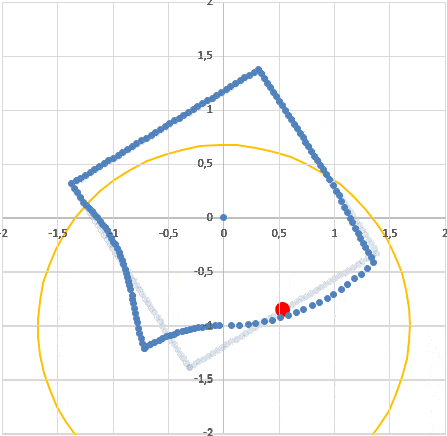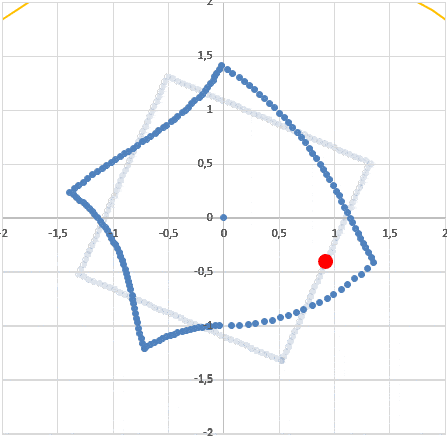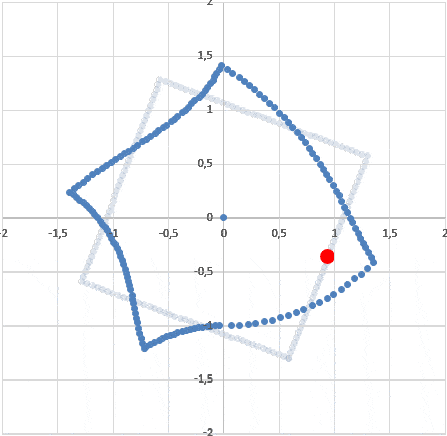
Для этого нужно сделать два шага. Во первых, нужно узнать, какие лучи света и от каких точек комнаты одновременно придут в ту же нижнюю точку, в которую придет и наблюдатель (чтобы их там увидеть). Для этого проще всего использовать прием обратного времени: поставим наблюдателя с комнатой в нужном положении, а затем будем вращать комнату в обратном направлении и одновременно выпустим из точки наблюдателя световой круг. Все части комнаты, которые попадают внутрь круга, "замораживается". Нетрудно видеть, что если мы прокрутим теперь эту сцену в нужном направлении, то свет от всех точек "замороженной комнаты" как раз одновременно попадает в точку, в которую попадает и наблюдатель:


Второе. Такую картину видел бы наблюдатель, неподвижный в красной точке. Но наш наблюдатель имеет там мгновенную скорость, направленную влево (вращение комнаты по часовой стрелке). Нужно привести картинку неподвижного наблюдателя к картинке движущегося. Применим тот же прием: запустим полученную "кляксу" влево со скоростью наблюдателя (в обратном времени) и снова пустим круг света. Полученная картина - это как раз то, как наш вращающися в комнате наблюдатель видит эту комнату:

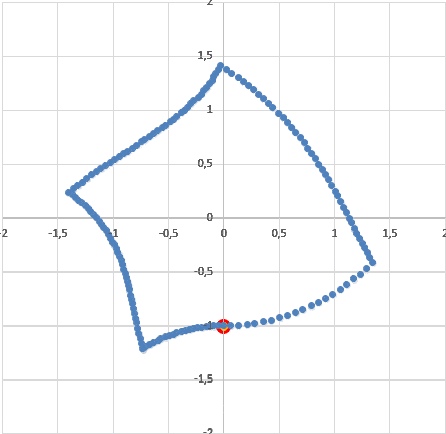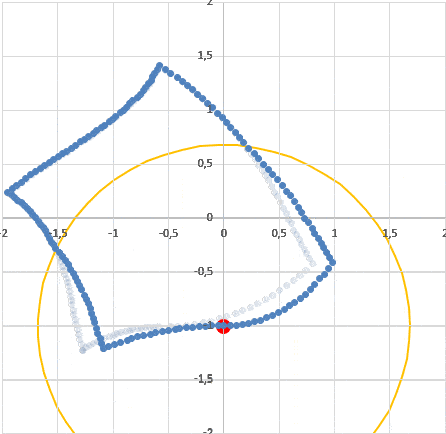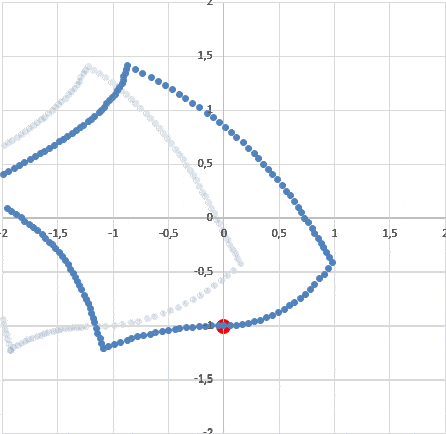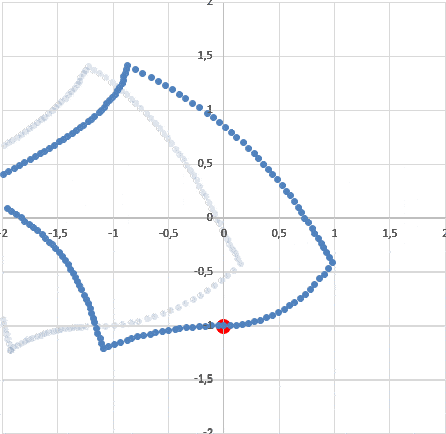
Хорошо видно, что наблюдатель легко может по одному ее внешнему виду понять, куда она вращается. Т.е. он не говорит о ее вращении. Он говорит о том, что в этой комнате есть определенная асимметрия. Примерно то же, что и проявление силы Кориолиса во вращающихся системах отсчета, которые вносят асимметрию в процессы в таких системах. Скажем, если двигаться в таких вращающихся системах по кругу вокруг центра по часовой стрелке, то сила Кориолиса направлена к центру (допустим), а если двигаться против часовой стрелки - то от центра

Такими же методами можно узнать и красное смещение, которое наблюдатель будет видеть.

Тут еще нужно добавить, что мы рассматриваем здесь не квадратную комнату, которую раскрутили, а вращающийся объект, который в каждый момент времени в нашей не вращающейся СО представляет собой квадратную комнату. Т.е. если этот вращающийся объект, скажем, плоский и двумерный, и мы снимаем его на фото перпендикулярно ее плоскости с далекого расстояния, то всегда видим, что на фото - квадратная комната.

Вопрос о том, что будет происходить с реальной квадратной комнатой, которую раскручивают - он более сложный. Это задача чисто кинематическая: задано движение точек, нужно вычислить, как оно выглядит для такого-то наблюдателя.

[Poehavchij]

sergey zhukov
Мне кажется, я могу сильно ошибаться конечно, но то что вы описали это то что видит наблюдатель в классической физике в очень большой комнате, в которой свет распространяется долго, и тут нет эффектов СТО/ОТО, а просто тот факт что свет распространяется с конечной скоростью

[sergey zhukov]

Poehavchij
Верно.
Тем не менее это и есть то, что будет видеть наблюдатель внутри вращающейся комнаты, если только мы согласны, что вращающаяся комната - это вращающийся объект, который в каждый момент времени в нашей не вращающейся ИСО выглядит (лучше, наверное, говорить "фиксируется", чтобы отличать это от картинки, которую мы видим), как комната. Вся сложность находится внутри этого последнего предположения: что нужно делать с реальным телом (и каким оно должно быть в условиях неподвижности), чтобы оно так выглядело в нашей неподвижной ИСО при вращении? Какие силы и как к нему потребуется приложить? Какие напряжения и деформации в нем возникнут? Будет ли пространство-время вообще оставаться плоским в этом случае? Мы этим не занимаемся, а просто говорим: в плоском пространстве-времени задано такое-то движение. Просто принимаем это за исходные данные. Поэтому это задача кинематическая (задано движение, а силы, которые его обеспечивают, мы не рассматриваем).

Что происходит с настоящей комнатой, которую начинают вращать все быстрее, во что она превратится и остается ли здесь пространство-время плоским - это более сложный вопрос.

Тут происходит примерно то же, что в следующем случае. Допустим, мы взяли квадратную комнату и ускорили ее до некоторой скорости $u$. В неподвижной СО она сплющилась и стала представлять собой, скажем, прямоугольник. Мы можем подсчитать степень этого сплющивания (эффект СТО), а затем (взяв уже прямоугольную комнату вместо квадратной) вычислить при помощи вот таких картинок, как мы, находящиеся в неподвижной СО, будем видеть эту комнату в движении.

Но можно и просто сказать: дано, что движется некий объект прямоугольного вида. Вычислить, как он будет виден для нас. Как этот объект выглядит в неподвижном виде? Нас это не волнует. Может, это квадратная комната. Может, прямоугольная. Может быть, такой объект в "в неподвижном виде" вообще не может существовать (как в случае с вращением).

[Georgii]

Отвечаю на первый вопрос в теме. ИСО - это выделенные по отношению к остальным системы отсчёта, так как к ним применяются конкретные требования физического характера. Из-за этих требований переход от одной ИСО к другой ИСО должен подчинятся определённым правилам, порой нетривиальным. К неинерциальным системам отсчёта таких требований нет, "они никому ничего не должны". Поэтому преобразование в неинерциальную систему отсчёта не должно в себе содержать никаких сложностей. Берёшь и вращаешь её. Нет требований - нет проблем