Посмотрите, пожалуйста, последнее сообщение.
Оба цитата из вашего последнего сообщения #1696119
Ой, извините, не то сообщение скопировала.
Спасибо большое за интерес к моим попыткам.

Сейчас перепишу нормально.
-- Сб авг 02, 2025 13:20:10 --Ферма утверждал, что уравнение

не имеет решений в рациональных числах.
Попробуем доказать обратное.
Предположим, что такое решение существует
при

,

,

, где

,

,

- целые положительные взаимно простые числа и

, то есть

.
1.1.

, где

- целое положительное число

, где

- целое положительное число.
1.2.

,

Перемножаем левые и правые части, получаем:

,

1.3.

,

(п.1.1). Перемножаем левые и правые части, получаем:

, следовательно,

.
2.1.1 функция

в точках

и

принимает одинаковые значения разных знаков и она является целой рациональной функцией, непрерывна и определена при всех значениях

, следовательно, между

и

существует точка ( назовем ее

, значение функции в которой равно

.
2.1.3 Найдем все точки, значение функции в которых равно нулю.

.

или


, отсюда

или

.
Поскольку

,

,

-рациональное число.
3.1.1 поскольку
функция

является целой рациональной функцией, непрерывна и определена при всех значениях

и ее значение равно нулю в точках 0, h и с,
существует три точки, в которых она принимает одинаковые отрицательные значения (

,

и

) и три , в которых она принимает одинаковые положительные значения (

,

и

).
Эти числа действительные (поскольку если они они комплексные, Это противоречит существованию рационального

между

и

Очевидно, что может существовать два варианта расположения

относительно

- точки перегиба функции (

и


и
три варианта расположения

,

,

,

относительно друг друга:

,

,

.
4.1
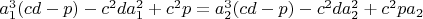
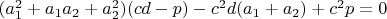
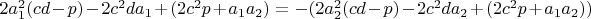
При этом
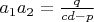
, где

-целое число.
Тогда
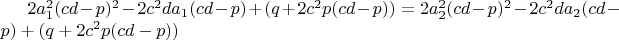
4.2. Функция
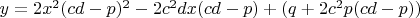
является целой рациональной функцией, непрерывна и определена при всех значениях

Найдём критические точки
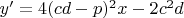
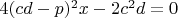
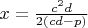
В точках

и

она принимает одинаковые значения разных знаков, следовательно, критическая точка находится между этими двумя точками.
Аналогично с

и

:
5.1
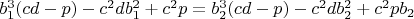
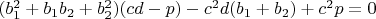
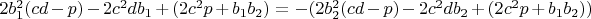
При этом
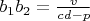
, где

-целое число.
Тогда
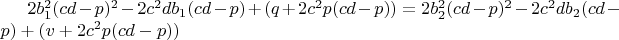
5.2. Функция
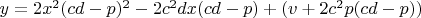
является целой рациональной функцией, непрерывна и определена при всех значениях

Найдём критические точки
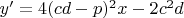
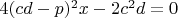
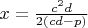
В точках

и

она принимает одинаковые значения разных знаков, следовательно, критическая точка находится между этими двумя точками.
Но это невозможно, поскольку
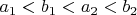
(то же самое с парами

и

,

и

,

и

,

и

, но я не знаю ( простите мою дремучесть), можно ли рассматривать функции с иррациональным свободным членом.
Но мы получаем, что не может быть таких пар, чтобы между ними всеми была точка
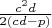
Если есть какое-то рациональное зерно в моих рассуждениях, я распишу подобно
-- Сб авг 02, 2025 13:25:04 --nnosipovКак я рада вас видеть! Буду очень благодарна, если вы посмотрите
