Since
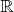
is the only open set that can cover

, any open cover of
![$[-1, 1]$ $[-1, 1]$](https://dxdy-01.korotkov.co.uk/f/4/3/c/43ca5ad9e1f094a31392f860ef481e5c82.png)
would necessarily have to contain
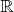
. But then
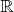
alone is enough to cover
![$[-1, 1]$ $[-1, 1]$](https://dxdy-01.korotkov.co.uk/f/4/3/c/43ca5ad9e1f094a31392f860ef481e5c82.png)
?
This is correct.
To give you an example of accurate argument, I shall rewrite the latter argument in a very detailed way.
"Prove that
![$[-1,1]$ $[-1,1]$](https://dxdy-03.korotkov.co.uk/f/6/9/9/699628c77c65481a123e3649944c0d5182.png)
is a compact subset in topology
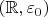
. Suppose that
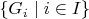
is a cover of
![$[-1,1]$ $[-1,1]$](https://dxdy-03.korotkov.co.uk/f/6/9/9/699628c77c65481a123e3649944c0d5182.png)
by open sets (here

is some set, indexing elements of the cover). We have to prove that this cover contains a finite sub-cover covering
![$[-1,1]$ $[-1,1]$](https://dxdy-03.korotkov.co.uk/f/6/9/9/699628c77c65481a123e3649944c0d5182.png)
.
As
![$0\in[-1,1]$ $0\in[-1,1]$](https://dxdy-03.korotkov.co.uk/f/e/1/4/e142507c5deb636a050a805d173d1f8b82.png)
, there exists an element of the cover,
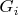
, containing

. But the only open set in the topology
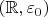
, containing

, is
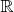
. Therefore,
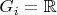
for some
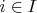
. Since
![${\mathbb R}\supset [-1,1]$ ${\mathbb R}\supset [-1,1]$](https://dxdy-03.korotkov.co.uk/f/e/f/f/eff3f27105381cab6c67b0b3ed2768c582.png)
, we see that the cover
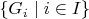
contains a finite set of elements (in fact, a single element) covering
![$[-1,1]$ $[-1,1]$](https://dxdy-03.korotkov.co.uk/f/6/9/9/699628c77c65481a123e3649944c0d5182.png)
. "



