But I guess since the open sets are not ordered we could just the drop the indexing.
Yes, correct.
By
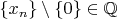
I meant to denote a rational sequence missing

. Maybe
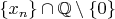
would've worked better.
No, this formula makes no sense also. As the colleague said already, the correct formula is
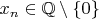
, or
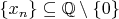
,
or
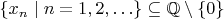
. But to avoid any possible misunderstandings, usually a mix of symbolic and natural language is used, for example " Let
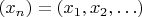
be a sequence of rational numbers different from zero", or "

be a sequence of rational numbers
such that
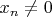
for all

", and the same can be expressed in many other ways also.
Of course, the rest of the proof also should be written clearly.
I would like to inform you about several more elementary books on topology, they may be useful for you. These books are written in a more classical style, with more details, than McCluskey.
W.G.Chinn, N.E.Steenrod, First concepts of topology
B.Mendelson, Introduction to topology
S.A.Morris, Topology without tears(These books may be found at the so called "libgen" cite, which is now at url "libgen.rs". But this is a pirate resourse, so it may change its location).
-- 07.06.2024, 03:08 -- and has no convergent subsequence.
This is correct, but this should be proved.



